
안녕하세요, HELLO
각 실험에서 발생 가능한 결과가 단 2가지인 베르누이 시행에서, 기존에 정리한 이항분포, 초기하 분포 그리고 포아송 분포는 성공 결과에 대한 분포를 다뤘습니다. 반면에 기하 분포(geometric distribution)은 성공할 때까지 시행하는 경우에 실패(시행) 횟수의 분포를 다룹니다. 오늘은 기하 분포에 대해서 정리해 보겠습니다.
CHAPTER 1. '기하 분포(geometric distribution)' 선행 지식
CHAPTER 2. '기하 분포(geometric distribution)' 정리
CHAPTER 3. '기하 분포(geometric distribution)' 공식 및 특징
CHAPTER 1. '기하 분포(geometric distribution)' 선행 지식
'기하 분포'에 앞서서, '베르누이 시행'과 '이항분포'에 대해 내용 정리가 필요한 분들은 이전에 발행한 글을 참고해주시기 바랍니다.
2022.01.16 - [DATA_SCIENCE/통계 (Statistics)] - 베르누이 시행(Bernoulli trial) 정리, 공식, 특징
베르누이 시행(Bernoulli trial) 정리, 공식, 특징
안녕하세요, HELLO 각 실험에서 발생 가능한 결과가 (성공, 실패), (앞면, 뒷면) 등으로 단 2가지인 경우를 베르누이 시행(Bernoulli trial)이라고 합니다. 오늘은 독립 시행에 대표적인 베르누이 시행,
hyunhp.tistory.com
2022.01.16 - [DATA_SCIENCE/통계 (Statistics)] - 이항분포(Binomial distribution) 정리, 공식, 특징
이항분포(Binomial distribution) 정리, 공식, 특징
안녕하세요, HELLO 성공할 확률이 p인 베르누이 시행(각 실험에서 발생 가능한 결과가 단 2가지인 경우)를 n 번 반복했을 때 성공 횟수(X)의 분포를 이항분포 (binomial distribution)이라고 합니다. 오늘
hyunhp.tistory.com
CHAPTER 2. '기하 분포(geometric distribution)' 정리
기하 분포는 베르누이 시행을 성공할 때까지의 실패(시행) 횟수의 분포를 의미합니다. 이항분포, 초기하 분포 그리고 포아송 분포에서는 성공한 횟수에 관심을 가졌으나 어떤 경우에는 시행 횟수에 관심을 가질 때가 있습니다. 이런 경우에는 기하 분포를 활용합니다. 기하 분포를 따르는 확률 질량 함수는 아래와 같이 정의되며, 초항이 p이며, 공비가 (1-p)인 '등비급수'의 형태로 정리됩니다.

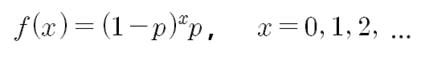
기하 분포에서 X는 성공할 때까지 시행했을 때의 '실패한 횟수'를 의미합니다. Y는 '성공할 때까지 시행한 횟수'를 의미합니다. 이 둘의 관계는 Y=X+1의 관계를 이룹니다. 이를 바탕으로 Y에 대한 확률 질량 함수는 아래처럼 정리됩니다.

CHAPTER 3. '기하 분포(geometric distribution)' 공식 및 특징
기하 분포에 따라 x 번째 시행에 성공할 확률 (x-1 번째까지 실패할 확률)은 아래와 같으며,

역으로 x+1번째 시행 이후로 성공할 확률 (x 번째까지 실패할 확률)은 전체 확률 1에서 x 번째 시행에 성공할 확률을 빼면 됩니다.

위에서 정리한 내용을 바탕으로 기하 분포의 시행에서 x 번째까지 실패하고, 다음 (x+1) 번째 시행에서 성공할 확률은 독립 시행과 동일하게 성공할 확률 p가 됩니다.

이전까지 시행된 결과에 무관하게 다음 시행 확률에 영향을 주지 않는 것을 무기억성 (memoryless)라고 하며, 이산형 분포에서는 기하 분포, 연속형 분포에서는 지수 분포가 무기억성 특징을 가지고 있습니다.
이어서 기하 분포의 기댓값은 무한등비급수의 합을 통해서 계산할 수 있습니다.
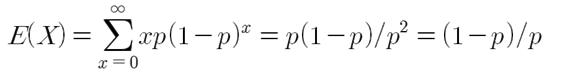
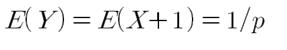
이때 X는 실패한 횟수, 그리고 Y는 시행한 횟수입니다. 기하 분포는 시행이 성공할 때까지의 실패 확률 그리고 시행 횟수를 고려하기에, 위에서 정리한 것처럼 시행 횟수는 실패한 횟수에 1을 더한 값(Y=X+1)이 됩니다.
■ 마무리
'기하 분포'의 공식 및 특징 등에 대해서 정리해봤습니다.
그럼 오늘 하루도 즐거운 나날 되길 기도하겠습니다
좋아요와 댓글 부탁드립니다 :)
감사합니다.
'STUDY > Statistics' 카테고리의 다른 글
| 다항 분포 (Mulitinomial distribution) 정리, 공식, 특징 (0) | 2022.01.16 |
|---|---|
| 음이항 분포(Negative Binomial Distribution) 정리, 공식, 특징 (1) | 2022.01.16 |
| 포아송 분포(Poisson distribution) 정리, 공식, 특징 (0) | 2022.01.16 |
| 초기하 분포(Hypergeometric distribution) 정리, 공식, 특징 (0) | 2022.01.16 |
| 이항분포(Binomial distribution) 정리, 공식, 특징 (0) | 2022.01.16 |




댓글