
안녕하세요, HELLO
확률(Probability)은 특정 사건이 일어날 가능성을 나타내는 비율로, 0과 1사이로 1을 넘을 수 없고, 음수가 될 수 없습니다. 확률 1은 사건이 항상 일어나는 것을 의미하고, 확률 0은 절대로 일어나지 않음을 의미합니다.
오늘은 확률(Probability)에 대해서 알아보고자 합니다.
CHAPTER 1. '확률' 정리
CHAPTER 2. '확률의 공리적 정의' 정리
CHAPTER 1. '확률' 정리
1. 확률의 고전적 정의
확률을 정의하는 역사적인 방법은 동전 던지기, 주사위 등처럼 유한한 표본공간에서, 가능한 모든 실험 결과들이 확률로 나타나는 경우를 뜻합니다. 고전적 정의에 따라 사건 A의 확률을 고전적 확률이라고 하며, 표현하면 아래와 같이 나타납니다. 표본공간에 속한 대상이 무한할 수도 있고, 모두 같은 확률을 갖는다는 가정이 맞지 않는 경우에는 고전적 확률을 정의하는 것이 어렵습니다.

2. 상대도수를 이용한 확률 정의
상대도수(relative frequency)의 극한을 사용하는 방법입니다. 어떤 실험을 1회 시행하면, 표본공간 S 내에서 사건 A가 일어나든지 아니면 일어나지 않든지, 둘 중에 하나가 됩니다. 이러한 실험을 동일한 조건에서 독립적으로 n 회 반복했을 때, 사건 A가 나타는 횟수를 n(A)라 할 때, 사건 A의 상대도수를 다음과 같이 나타낼 수 있습니다.

이때 실험을 무한히 반복한다는 가정하에서 상대도수의 극한값은 사건 A가 일어날 확률 P(A)로 정의됩니다.

상대도수를 이용한 확률은 고전적 정의의 한계점인 표본공간이 무한하거나 실험 결과들이 동일한 확률로 일어나지 않는 경우에도 적용될 수 있지만, 무한 반복 시행이 가능하지 않다는 등의 사건에 대해서는 정의가 무의미한 한계점이 있습니다.
3. 주관적 확률 정의
확률의 주관적 정의는 개인의 경험이나 지식, 정보, 직관 등을 토대로 각자의 주관에 따라 확률을 정해집니다. P(A)를 A라는 사건이 일어나는 것에 대한, 주관적인 믿음의 척도를 이용하여 확률을 정하는 방법입니다. 이후에 베이지안(Bayesian) 통계의 근간이 되는 정의입니다.
4. 확률의 공리적 정의
20세기 초반 러시아 수학자 안드레이 콜모고로프(A. N. Kolmogorov)는 공리적 방법을 이용해 확률을 정의했습니다. 공리적 정의는 고전적 확률, 통계적 확률이 가지는 특성을 모두 포함합니다. 공리는 수학에서 증명을 하지 않기로 약속한, 즉 당연한 것으로 가정하는 명제를 의미합니다. 확률을 공리적으로 정의한다는 것은 확률의 성질 중에 당연한 사실에 대해서 정리한 것입니다. 확률의 공리적 정의는 아래와 같습니다.

공리적 접근 방식에 의하면 확률이란 표본공간을 정의역으로 하면서, 위의 세 공리를 모두 만족하는 함수로 정의됩니다. 고전적 확률 정의, 상대도수를 이용한 확률 정의 또는 주관적 확률의 정의 등 각기 다른 방법으로 확률이 정의되더라도 위의 공리는 반드시 만족되어야 합니다.
추가적으로 공리에 근거한 확률의 성질에는 다음 정리와 같은 것들이 포함됩니다.

그리고 확률의 공리적 정의에 대해서 아래에서 자세하게 확인하고자 합니다.
CHAPTER 2. '확률의 공리적 정의' 정리
위에서 정리된 3개의 공리를 바탕으로 확률에 대해 아래와 같이 정리할 수 있습니다.

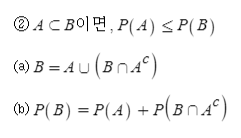


위에서 확인한 부울의 부등식 (Boole's inequality)는 합집합의 상한 값의 범위를 확인할 수 있으며, 반면에 본페로니 부등식 (Bonferroni’s inequality)은 교집합의 하한 값의 범위를 확인할 수 있습니다.
■ 마무리
'확률 (probability)'의 공식, 특성에 대해서 알아봤습니다.
그럼 오늘 하루도 즐거운 나날되길 기도하겠습니다
좋아요와 댓글 부탁드립니다 :)
감사합니다.
'STUDY > Statistics' 카테고리의 다른 글
| 확률변수 (Random vairable), 확률분포 (Probability distribution) 정리, 공식, 특징 (0) | 2022.01.14 |
|---|---|
| 독립 사건 (Independent event) 정리, 공식, 특징 (2) | 2022.01.14 |
| 조건부 확률 (conditional probability) 정리, 공식, 구조 (0) | 2022.01.13 |
| 지수함수, 로그함수, 삼각함수, 역삼각함수 정리, 공식, 구조 (1) | 2022.01.13 |
| 함수(Function) 정리, 공식, 구조 (0) | 2022.01.13 |




댓글