
안녕하세요, HELLO
결합 분포 (joint distribution)는 두 개 이상의 확률변수들을 동시에 고려한 확률분포입니다. 이번에는 두 개 이상의 확률변수들을 고려한 확률 구조인 결합 분포에 대해서 정리하고자 합니다.
CHAPTER 1. '결합 분포 (joint distribution)' 선행 지식
CHAPTER 2. '결합 분포 (joint distribution)' 정리
CHAPTER 1. '결합 분포 (joint distribution)' 선행 지식
'결합 분포'에 앞서서, '확률변수, 이산확률변수, 연속확률변수'에 대해 내용 정리가 필요한 분들은 이전에 발행한 글을 참고해주시기 바랍니다.
확률변수 (Random vairable), 확률분포 (Probability distribution) 정리, 공식, 특징
안녕하세요, HELLO 표본공간의 값을 실함수로 표현한 것을 확률변수 (random variable)라고 하며, 확률변수에서 표본공간의 값에 대한 확률을 표시한 것을 확률분포 (probability distribution)라고 합니다.
hyunhp.tistory.com
이산확률변수 (Discrete random variable), 연속확률변수 (Continuous random variable) 정리, 공식, 특징
안녕하세요, HELLO 이산확률변수 (discrete random variable)는 확률변수 X가 유한하여 셀 수 있는 확률변수입니다. 이산확률변수의 예로 '주사위를 던질 때 나올 수 있는 수'와 '한 개의 주사위를 두 번
hyunhp.tistory.com
CHAPTER 2. '결합 분포 (joint distribution)' 정리
□ 이산확률변수의 결합확률질량함수 (joint probability mass function)
두 이산확률변수 X와 Y에 대해, 동시에 X가 임의의 x 일 확률과 Y과 임의의 y 일 확률에 대해 결합확률질량함수 (joint probability mass function)를 f(x, y)로 표현할 수 있습니다.

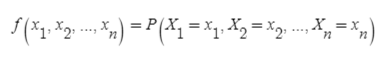
그리고 결합확률질량함수는 두 개 이상의 확률변수들의 확률분포는 0부터 1 사이에 값을 가지고, 전체 확률분포는 1을 가집니다.

□ 연속확률변수의 결합확률밀도함수 (joint probability density function)
두 연속확률변수 X, Y에 대해, 결합확률밀도함수 (joint probability density function)인 f(x, y)는 x와 y에서의 밀도를 나타내며, 아래의 성질을 만족합니다.

추가적으로, 결합확률밀도함수의 한 지점에서의 확률은 연속확률변수와 동일하게 0 값을 가집니다. 왜냐하면 한 지점에서의 밀도는 0을 나타내기 때문입니다.

두 개의 연속확률변수 X, Y에 대하여, X는 0부터 u까지 발생 가능성이 동일하며, Y는 0부터 v까지 발생 가능성이 동일하다면, 결합확률밀도함수는 1/uv 값을 가집니다. 결합확률밀도함수는 해당되는 위치에서 얼마나 밀집되어 있는지를 나타내는 것을 높이로 표현합니다. 발생 가능성이 동일한 연속확률변수의 확률분포는 아래와 같은 육면체의 모습을 가집니다.

이때, 부피는 가로, 세로, 높이의 곱으로 구해지며, 결합확률밀도함수의 전체 확률분포는 1 값을 가지기에, 가로 (u), 세로 (v)의 곱이 1이 되려면, 높이는 1/uv 값을 가지게 됩니다. 이는 f(x, y)가 해당 구간 안에서는 이런 형태의 높이를 가지는 것으로 표현할 수 있습니다.

■ 마무리
'결합 분포'의 공식 및 특징 등에 대해서 정리해봤습니다.
그럼 오늘 하루도 즐거운 나날 되길 기도하겠습니다
좋아요와 댓글 부탁드립니다 :)
감사합니다.
'STUDY > Statistics' 카테고리의 다른 글
| 왜도(skewness), 첨도(kurtosis) 정리, 공식, 특징 (0) | 2022.01.15 |
|---|---|
| 산포(Dispersion) 정리, 공식, 특징 (0) | 2022.01.14 |
| 이산확률변수 (Discrete random variable), 연속확률변수 (Continuous random variable) 정리, 공식, 특징 (0) | 2022.01.14 |
| 확률변수 (Random vairable), 확률분포 (Probability distribution) 정리, 공식, 특징 (0) | 2022.01.14 |
| 독립 사건 (Independent event) 정리, 공식, 특징 (2) | 2022.01.14 |




댓글