
안녕하세요, HELLO
통계분석은 모집단의 중심 위치를 기준으로 대칭(symmetric)이라고 가정합니다. 이에 따라 통계분석의 적절성은 대칭이란 가정을 해당 자료가 얼마나 만족하고 있는지에 따라 영향을 받습니다. 이러한 모집단의 대칭성을 확인하기 위해, 왜도(skewness) 그리고 첨도(kurtosis)를 활용합니다.
오늘은 수치자료 분포의 형태를 알아보는 왜도(skewness)와 첨도(kurtosis)에 대해서 알아보겠습니다.

CHAPTER 1. '왜도(skewness), 첨도(kurtosis)' 선행 지식
CHAPTER 2. '왜도(skewness), 첨도(kurtosis)' 정리
CHAPTER 1. '왜도(skewness), 첨도(kurtosis)' 선행 지식
'왜도와 첨도'에 앞서서, 자료 분포의 형태인 '산포(dispersion)'에 대해 내용 정리가 필요한 분들은 이전에 발행한 글을 참고해주시기 바랍니다.
2022.01.14 - [DATA_ANALYSIS/통계 (Statistics)] - 산포(Dispersion) 정리, 공식, 특징
산포(Dispersion) 정리, 공식, 특징
안녕하세요, HELLO 산포(Dispersion)는 자료들이 얼마나 퍼져 있는지를 나타내는 측도입니다. 자료의 분포가 조밀한 경우에는 중심 위치(평균)의 변동성이 작아지고, 넓게 분포된 경우에는 중심 위
hyunhp.tistory.com
CHAPTER 2. '왜도(skewness), 첨도(kurtosis)' 정리
□ 왜도(skewness)
왜도(skewness)는 자료가 대칭적으로 분포되어 있는지 또는 한쪽으로 치우쳐져 있는지에 대한 측도(measure)를 나타냅니다. 그래프의 모양이 아래처럼 오른쪽으로 뻗거나 또는 왼쪽으로 뻗어있는 경우에 왜도가 큽니다.

왜도(γ1)는 피어슨(Karl Pearson) 제안을 통해 아래와 같이 구할 수 있으며,
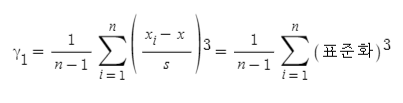
편차(표준화)의 세제곱은 평균보다 크면 양수가 그리고 작으면 음수가 되어, 평균에서 멀어질수록 편차는 큰 영향을 받아서 더욱 큰 양수 및 음수가 됩니다. 반면에 그래프가 좌우가 비슷한 형태를 가지면, 음수와 양수가 상쇄되어 γ1은 0에 근접한 값을 가지게 되고, γ1이 0이면 그래프가 대칭임을 나타냅니다.
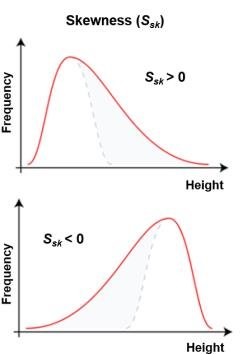
위에 그림처럼 오른쪽 꼬리가 긴 경우에는 큰 양수 값을 가지며, 이를 양의 왜도(positive skewness), skewed to the right라고 하며, 반면에 아래 그림처럼 왼쪽 꼬리가 긴 경우에는 큰 음수 값을 가지고, 음의 왜도(negative skewness), skewed to the left라고 합니다. 그리고 왜도가 큰, 즉 꼬리가 길게 분포된 형태를 두터운 꼬리, heavy tail이라고 합니다
□ 첨도(kurtosis)
첨도(kurtosis)는 양쪽 꼬리의 두터움 정도를 나타내는 값입니다. 첨도는 큰 편차 또는 이상치(outlier)가 많을수록 큰 값을 나타냅니다.

첨도(γ2)는 피어슨(Karl Pearson) 제안을 통해 아래와 같이 구할 수 있으며,

편차의 네제곱은 평균에서 멀어질수록 큰 값을 가지게 됩니다. 이를 통해 분포의 중심보다 꼬리 부분에 자료가 모여있는지, 즉 그래프의 모양이 두꺼울수록 영향을 많이 받게 됩니다. 이론적으로 정규분포의 첨도 값은 3입니다. 이에 따라 첨도 값이 3보다 작을 경우에는 산포(dispersion)는 정규분포보다 꼬리가 얇은 분포로 생각할 수 있습니다. 반면에, 첨도 값이 3보다 큰 양수이면 정규분포보다 꼬리가 두꺼운 분포로 판단할 수 있습니다.
■ 마무리
자료의 분포 형태를 측정하는 '왜도(skewness) 그리고 첨도(kurtosis)'의 공식 및 특징 등에 대해서 정리해봤습니다.
그럼 오늘 하루도 즐거운 나날 되길 기도하겠습니다.
좋아요와 댓글 부탁드립니다 :)
감사합니다.
'STUDY > Statistics' 카테고리의 다른 글
| 공분산(covariance) 정리, 공식, 특징 (0) | 2022.01.16 |
|---|---|
| 분산(variance), 표준편차(standard deviation) 정리, 공식, 특징 (0) | 2022.01.16 |
| 산포(Dispersion) 정리, 공식, 특징 (0) | 2022.01.14 |
| 결합 분포 (Joint distribution) 정리, 공식, 특징 (0) | 2022.01.14 |
| 이산확률변수 (Discrete random variable), 연속확률변수 (Continuous random variable) 정리, 공식, 특징 (0) | 2022.01.14 |




댓글