
안녕하세요, HELLO
분산(variance)은 자료가 퍼져 있는 정도를 나타나는 통계값이며, 편차의 제곱합을 통해 구할 수 있습니다. 원래 자료의 측정 단위가 제곱이 되기에, 이를 조정하기 위해 분산에 제곱근을 취한 통계값이 표준편차(standard deviation)입니다. 오늘은 분산과 표준편차에 대해서 살펴보려고 합니다.
CHAPTER 1. '분산(variance)과 표준편차(standard deviation)' 선행 지식
CHAPTER 2. '분산(variance)과 표준편차(standard deviation)' 정리
CHAPTER 3. '분산(variance)과 표준편차(standard deviation)' 공식 및 특징
CHAPTER 1. '분산(variance)과 표준편차(standard deviation)' 선행 지식
'분산(variance)과 표준편차(standard deviation)'에 앞서서, 데이터가 퍼져있는 정도를 나타내는 통계값인 '산포(dispersion)'에 대해 내용 정리가 필요한 분들은 이전에 발행한 글을 참고해주시기 바랍니다.
2022.01.14 - [DATA_ANALYSIS/통계 (Statistics)] - 산포(Dispersion) 정리, 공식, 특징
산포(Dispersion) 정리, 공식, 특징
안녕하세요, HELLO 산포(Dispersion)는 자료들이 얼마나 퍼져 있는지를 나타내는 측도입니다. 자료의 분포가 조밀한 경우에는 중심 위치(평균)의 변동성이 작아지고, 넓게 분포된 경우에는 중심 위
hyunhp.tistory.com
CHAPTER 2. '분산(variance)과 표준편차(standard deviation)' 정리
□ 분산(variance)
분산(variance)은 자료가 퍼져 있는 정도를 나타나는 통계값으로, 편차의 제곱합을 통해 구할 수 있습니다. 표본의 크기를 n, 표본이 가질 수 있는 값을 {x1, x2, ..., xk}인 표본분산(sample variance)은 아래처럼 구할 수 있습니다.

이때 n을 계속 크게 하면 표본이 모집단이 되며, 아래처럼 표본분산이 모분산(population variance)으로 수렴합니다.
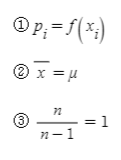
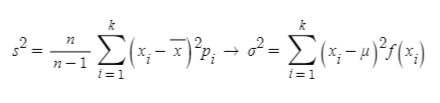
□ 표준편차(standard deviation)
확률변수 X의 분산을 Var(X)로 표시하며, Var(X)는 아래처럼 정의됩니다. 분산은 자료의 측정 단위가 제곱이 되기에, 이를 조정하기 위해 분산에 제곱근을 취한 통계 값인 표준편차 (standard deviation)는 분산에 제곱근을 취합니다.
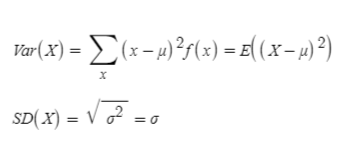
이산확률변수 X의 분산 Var(X)는 아래와 같습니다.
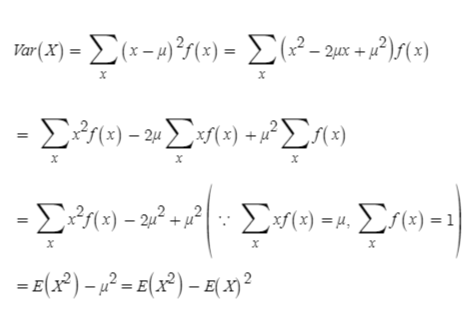
연속확률변수 X의 분산 Var(X)는 아래와 같습니다.

CHAPTER 3. '분산(variance)과 표준편차(standard deviation)' 공식 및 특징
확률변수 X가 곱해지거나, 더해지는 등 표본이 바뀌는 경우에, 분산은 위치의 변화를 주는 더하거나 빼는 연산은 분산에 영향을 주지 않지만, 변수에 곱해지는 값은 영향을 줍니다. 이를 바탕으로 정리된 분산의 성질은 아래와 같습니다.
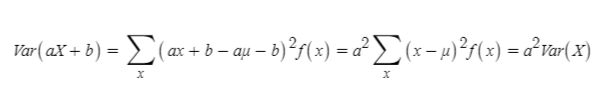
추가적으로, 표준편차의 곱연산은 절댓값을 취하면서 구해집니다.

■ 마무리
'분산(variance)과 표준편차(standard deviation)'의 공식 및 특징 등에 대해서 정리해봤습니다.
그럼 오늘 하루도 즐거운 나날 되길 기도하겠습니다
좋아요와 댓글 부탁드립니다 :)
감사합니다.
'STUDY > Statistics' 카테고리의 다른 글
| 상관계수(coefficient of correlation) 정리, 공식, 특징 (0) | 2022.01.16 |
|---|---|
| 공분산(covariance) 정리, 공식, 특징 (0) | 2022.01.16 |
| 왜도(skewness), 첨도(kurtosis) 정리, 공식, 특징 (0) | 2022.01.15 |
| 산포(Dispersion) 정리, 공식, 특징 (0) | 2022.01.14 |
| 결합 분포 (Joint distribution) 정리, 공식, 특징 (0) | 2022.01.14 |




댓글