
안녕하세요, HELLO
오늘은 길버트 스트랭 (Gilbert Strang) 교수님의 선형대수학 강의인 "MIT 18.06 Linear Algebra, Spring 2005"에 대해서 정리하려고 합니다. 선형대수학 강의에 대한 정리와 더불어, 딥러닝을 위한 선형대수학 관점에서도 접근하여 강의를 이해하고 분석하려고 합니다.
"MIT 18.06 Linear Algebra, Spring 2005"의 7주차 "Solving Ax = 0: pivot variables, special solutions"의 강의 내용입니다.
CHAPTER 1. 'Ax=0의 해(Null space) 계산'
CHAPTER 2. '기약행 사다리꼴 행렬(Reduced row echelon form)'
CHAPTER 1. 'Ax=0의 해(Null space) 계산'
이번 강의에서는 임의의 3x4크기의 직사각형 행렬(Rectangular Matrix) A로 진행해 보겠습니다.

Column 관점에서 살펴보면 column 2는 column 1의 2배로서, column 1과 column 2는 상호 종속적입니다(dependent). 다음은 row 관점에서 살펴보면 row 1과 row 2를 더하면 row 3가 됩니다. 따라서 row 3는 독립적이지 않습니다 (not independent).
이전 수업의 소거법은 정방행렬(square matrix)에 대해서만 진행했지만, 이번에는 직사각형 행렬(Rectangular matrix)에 대해 진행합니다. 또한 소거 과정에서 pivot의 위치에 0이 나왔을 때 처리하는 방법에 대해서도 살펴보겠습니다.
이번 강의는 Ax = 0의 해, 즉 Null space를 구하는 것입니다. Null space를 구하는 방법은 행렬 A를 소거(Elimination)하는 것입니다. 중요한 포인트는 소거를 하는 과정에서 Null space를 변화시키지 않는다는 것이다. 소거 과정에서 column space는 바꾸겠지만, 우변의 벡터가 모두 0이기에 결과적으로 봤을 때 그 과정에서 해의 집합인 Null space는 바뀌지 않습니다.
Ax=0의 방정식을 봤을 때 Null space는 좌변의 A행렬과 우변의 영벡터 b에 대한 방정식을 만족시켜야만 하는 해의 집합입니다. 소거 과정에서 행렬 A의 column space는 변할 수 있으나 본래의 A와 영벡터 b에 대한 방정식을 만족시키는 해의 집합 자체는 변하지 않습니다.
A의 첫 번째 pivot은 1입니다. pivot 바로 아래의 원소인 A(row2, col1)=2를 소거해야 하므로, row2 = row2 - 2*row1를 계산하면 식 (2)의 step1과 같이 됩니다. row3도 역시 소거를 하려면 row3 = row3 - 3*row1를 계산하면 step2와 같이 됩니다.
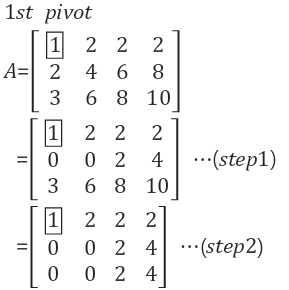
첫 번째 pivot의 아래에 있는 원소는 모두 0으로 만들어 소거했습니다. 이제 다음 stage인 column 2로 진행해 보겠습니다. 원래 같았으면 두 번째 pivot은 A(row2, col2)인데, 식(3)과 같이 값이 0이다. 이전 수업에서 배웠듯이 0인 원소는 pivot이 될 수 없습니다.
만약 두 번째 pivot의 아래의 원소 A(row3, col2)가 0이 아닌 값을 가진다면, 행 교환(row exchange)을 통해 pivot값을 바꿔서 설정해 주면 됩니다. 그러나 원소 A(row3, col2)가 0이기 때문에 결과적으로 column 2에서의 소거는 더 이상 진행되지 않습니다. 즉 두 번째 pivot은 column 2에 없습니다.
column 2에 원래 존재해야 할 pivot이 없는 이유는, 앞에서 살펴본 것처럼 A의 column 2는 column 1에 종속적(dependent)이기 때문입니다. 행렬 A를 보면 col1의 2배가 col2이며. 즉 두 column이 같은 선상에 위치한다는 의미입니다.
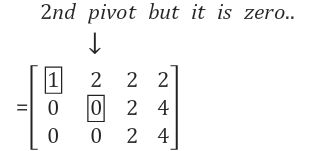
세 번째 column의 두 번째 row부터는 0이 아닌 값이 존재합니다. 결국 두 번째 pivot은 A(row2, col3)=2가 됩니다. 네 번째 column은 3 번째 pivot column에서 1번째 pivot column을 뺀 것에 2배를 하면 구할 수 있습니다. column 관점에서 pivot column을 구하게 되면, 1번째 그리고 3번째 column이 됩니다.
그리고 row 관점에서 생각하면, 두 번째 pivot을 기준으로 아래의 원소들을 0으로 만들 수 있습니다. 이때 아래의 row3와 pivot이 있는 row2는 같습니다. 따라서 row3=row3-1*row2가 됩니다. 이를 통해 1 번째 row와 2번째 row가 pivot row가 됩니다.
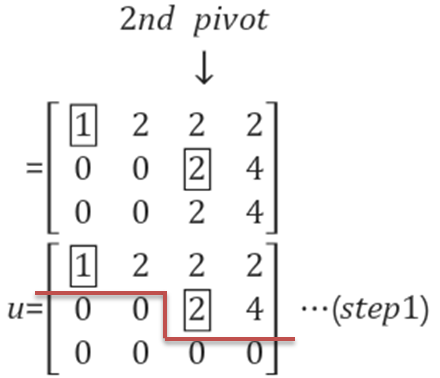
행렬의 모양이 상삼각행렬(Upper triangular matrix)처럼 삼각형 모양이 아니라 계단 형태입니다. 이를 echelon form이라고 정의합니다. 그리고 소거를 통해 알아낸 행렬 A의 "pivot의 개수(number of pivots)"의 개수는 2이다. 바로 pivot 개수가 의미하는 것은 행렬 A의 Rank입니다.
위 정리를 통해 우리는 아래처럼 정리할 수 있습니다.
- 임의의 행렬 A에 대해 U행렬을 얻기 위해 행렬 A를 소거(Elimination)한다. 소거 과정에서 pivot의 개수를 알아낼 수 있는데 이때 pivot의 개수가 바로 행렬 A의 Rank이다.
- Rank는 시스템 행렬 A의 선형 독립(Linearly independent)인 row 혹은 column vector의 수를 나타낸다. 이 Rank는 소거 과정에서 나타나는 pivot의 개수와 일치한다.
- Rank of A = number of pivots
□ Ux = 0의 해에 대한 계산
우리는 지금까지 Ax=0에 대한 해를 구하고자 했습니다. 이번에는 위에서 계산한 A를 소거한 행렬인 U에 대한 해, 즉 Ux=0를 구하고자 합니다.
다시 한번 정리하면, 해를 고려하지 않고 행렬을 기약사다리꼴 행렬로 계산하는 이유는 Ax = 0에 대해서 계산하기 때문입니다. 만약에 b가 아닌 해에 대해서 Ax = b를 구하게 된다면, 기약사다리꼴 행렬로 계산할 때 b를 고려해서 pivot을 구해야 합니다. 이러한 내용은 다음 강의 8강에서 다뤄집니다.
여기서 한 가지 염두해둬야 할 것은 Ax=0와 Ux=0의 해가 똑같은 Null space에 존재한다는 것이다. A를 소거하여 만든 행렬 U는 비록 A와 비교했을 때 column space는 변했겠지만 해는 동일한 Null space에 존재합니다. 이것이 앞단에서 말했던 소거과정에서 Null space는 바뀌지 않는다는 것을 의미합니다.
결국 Ax=0와 Ux=0의 해는 같은 Null space입니다.
Ux=0의 해는 Ax=0를 계산할 때와 같이 해는 존재하겠지만, 이번에는 pivot variable과 free variable로 살펴보겠습니다.
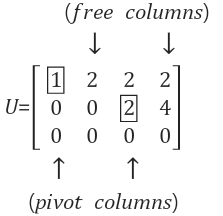
U행렬에서 소거 과정에서 찾았던 pivot이 있는 column이 pivot column이고, 이를 제외한 나머지 column이 free column입니다. free column으로 명명하는 이유는 Ux=0의 해를 구할 때 free column에 대응되는 변수에 우리가 원하는 임의의 값을 자유롭게 설정할 수 있기 때문입니다. free column은 2번째와 4번째이므로 solution 벡터 x에서 column 2와 column 4에 각각 곱해지는 x2와 x4에는 임의의 값으로 설정할 수 있습니다. 그런 다음 x1과 x3에 대해 해를 구하면 됩니다.
아래는 Ux=0에서 해(solution) x벡터를 나타냅니다. x2와 x4에 임의의 값을 설정할 수 있으며, 강의에서는 계산하기 편하도록 x2=1, x4=0으로 설정했습니다.
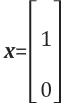
x의 free variable값을 설정했으니 이제 Ux=0에 대해서 풀어보겠습니다.
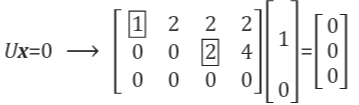
방정식으로 표현하면 U의 row3는 모두 0이기 때문에 제외하면 총 2개의 방정식을 가집니다.
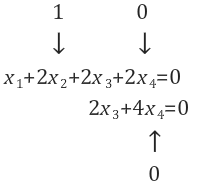
x2와 x4는 1과 0으로 각각 설정했습니다, 나머지 x1과 x3는 Lecture 2에서 배웠던 후방대입법(Back substitution)을 통해 값을 찾을 수 있습니다. x2=1, x4=0일 때, x3는 후방대입법을 통해 x3=0 임을 알 수 있습니다. 이제 x2=1, x3=0, x4=0을 통해 x1을 계산하면 -2를 구할 수 있습니다.
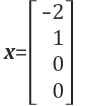
이 x가 바로 Ux=0의 해(solution)이며 Null space의 값 중 하나입니다. 또한 Ax=0의 해입니다. column picture형식으로 정리하면 아래와 같습니다.
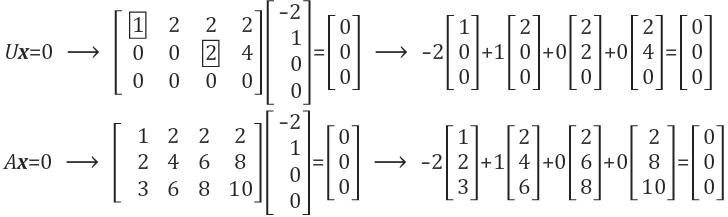
Ux=0에서 구한 해 x를 Ax=0에도 똑같이 적용해도 식이 성립하는 것을 볼 수 있습니다.
□ Null space 영역 계산
계산 A와 U에 대한 해 x는 Null space에 있습니다. 나머지 해는 임의의 상수 c를 x에 곱해주면 됩니다.
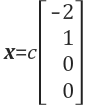
임의의 상수 c가 곱해진 해 x는 4차원 공간 R4에서 무한대의 2차원 line을 표현합니다. 이때 x는 분명 Null space상에 존재합니다. 하지만, 위의 식의 x는 A와 U에 대한 모든 Null space를 나타내지 않습니다. 행렬 A는 2개의 free variable을 가지고 있습니다. 즉 x2와 x4가 free variable인데, 우리는 x2=1, x4=0으로 결정했을 때의 해를 구한 것입니다. 다른 free variable인 x2=0, x4=1일 때의 해를 살펴보겠습니다.
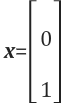
위와 같이 값을 설정하고 아까의 후방대입법(back substitution) 과정을 반복하면 됩니다.
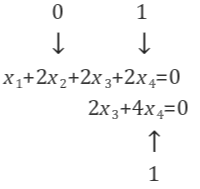
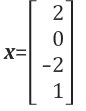
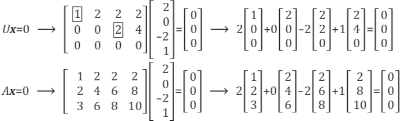
x가 선형방정식에서 의미하는 것은 2*col1+0*col2-2*col3+1*col4입니다. U와 A의 방정식에 각각 대입하여 계산해 보면 성립하는 것을 알 수 있습니다.
임의의 free variable을 설정하여 구한 해(solution)이며 이를 special solution이라고 합니다. 보통 special solution을 계산할 때는 첫 번째 free variable을 1로 놓고 나머지는 0, 그다음은 두 번째 free variable만 1로 놓고 나머지는 0으로 설정하는 식으로 계산합니다. 새로 구한 x에 관련된 나머지 해들도 역시 여기에 임의의 상수를 곱해주면 구할 수 있습니다.
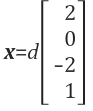
앞에서 계산한 Null space에서의 2개 벡터는 각각은 Null space상에 존재하고, 이들은 임의의 free variable을 설정하여 만들어진 해들의 집합입니다. 이를 통해 두 개의 해의 선형 결합(Linear combination)을 통해 전체 Null space를 정의할 수 있습니다.
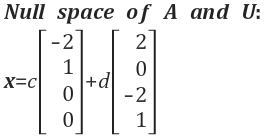
special solution은 각 free variable마다 존재합니다.
행렬 A의 rank가 2이고 rank는 pivot variable의 수임을 배웠습니다. pivot variable의 수는 m(rows) x n(columns) 행렬에서 column의 수인 n에 대해서 정의됩니다. free variable은 pivot을 뺀 나머지 column의 수가 될 것입니다. 즉 column의 수에서 rank의 수를 뺀 것과 같습니다.
즉, column의 수 4에서 rank의 수 2를 뺀 2가 최종적인 free variable의 수가 됩니다.
이를 정리하면 아래와 같습니다.
- 행렬 U는 두 개의 free variable을 가지고 있고 한 개의 free variable이 하나의 해(solution)에 대한 line을 표현했다고 생각하자. 이때 우리는 두 개의 free variable을 가지고 있기에 총 두 개의 line을 가지고 있으며 이 두 라인의 선형 결합으로 하나의 평면(plane)이 행렬 A의 Null space 전체를 표현하는 것이다.
지금까지 배운 알고리즘을 통해, 임의의 행렬 A의 모든 Null space를 구할 수 있습니다.
CHAPTER 2. '기약행 사다리꼴 행렬(Reduced row echelon form)'
행렬 A를 소거(elimination)하여 기약사다리꼴 행렬 U를 만들었습니다. 이때의 U는 계단 형태를 보였고 이를 echelon 형태라고 합니다. echelon 형태는 임의의 행렬에 가우스 소거법(Gauss Elimination)을 적용했을 때 계단 모양이 나오며, 몇 가지 조건을 만족하는 행렬을 의미합니다.
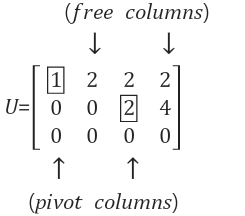
위에서 살펴본 U행렬을 잘 보면 세 번째 row가 전부 0인 것을 알 수 있습니다. 이는 소거 (elimination) 전의 행렬 A의 row3가 row1과 row2의 선형 결합이기 때문입니다. 결국 row3가 row1과 row2에 종속적(dependent)이기 때문에 소거를 한 행렬 U의 세 번째 row가 0이 되는 것입니다. 이러한 관계를 소거(Elimination) 작업을 통해 찾았습니다.
그다음에는 U행렬을 다시 한번 간소화해 보겠습니다. Gauss-Jordan 소거법을 통해, 아래에서 위쪽으로 소거를 진행합니다. 역방향(위쪽)으로 소거를 진행할 땐 pivot 원소의 위쪽에 있는 원소들을 소거하는 것입니다. 즉 기약행 사다리꼴 행렬(Reduced row echelon form matrix)은 pivot 원소들의 아래, 위로 모두 0이 되어야 합니다.
위의 행렬에서 pivot 원소가 두 개 존재합니다. 첫 번째 pivot (row1, col1)은 아래위로 모두 원소가 0입니다. 그러나 두 번째 pivot (row2, col3)은 위쪽 원소 (row1, col3)가 2로, 0이 아닙니다. 소거 방법은 소거할 원소가 pivot과 같기 때문에 1을 곱해서 빼주면 됩니다. 즉 row1 = row1 - row2를 진행하면 됩니다.
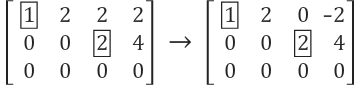
기약행 사다리꼴이 되기 위해 pivot 원소들을 모두 1로 만들어야 합니다. 첫 번째 pivot은 이미 1이므로 넘어가고, 두 번째 pivot을 1로 만들어야 합니다. 이는 pivot이 있는 row 전체를 pivot으로 나눠주면 됩니다.

이렇게 계산된 최종 R행렬이 기약 행 사다리꼴 행렬(Reduced row echelon form matrix)입니다.
결국 기약 행 사다리꼴 행렬(Reduced row echelon form)이 되기 위해선 다음의 조건들을 만족해야 합니다.
기약 행 사다리꼴 행렬 조건
- pivot 원소들은 반드시 1이 되어야 한다.
- pivot 원소가 있는 column에서 pivot 변수의 모든 아래/위 원소들은 0이 되어야 한다.
- 각 row는 처음 나오는 pivot 원소를 만나기 전까지 모든 원소가 0이어야 한다.
- 모든 원소가 0인 row는 반드시 pivot 변수가 있는 row의 밑에 있어야 한다.
□ 기약 행 사다리꼴 행렬 특징
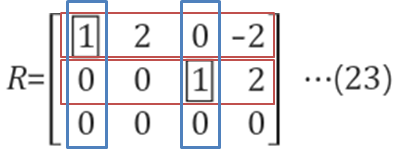
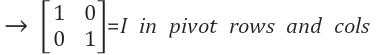
빨간색 box는 pivot row를, 파란색 box는 pivot column을 나타냅니다. 이 둘이 겹쳐지는 2x2 크기의 단위행렬의 모습을 확인할 수 있습니다. 단위행렬이 나타나는 이유는, 행렬 A를 소거하는 과정에서 pivot variable의 위/아래의 모든 원소를 0으로 맞추었고, 모든 pivot을 1이 되도록 만들었기 때문입니다.
가우스 소거법을 반복해서 적용하여 처음 A행렬에서 U행렬을 만들었고, 그리고 최종적으로 R행렬을 만들었습니다.

행렬 A에서 U로 행렬을 변환한 뒤에도, Ax=0와 Ux=0의 해는 동일한 Null space에 존재함을 알았습니다. 그리고 행렬 U를 소거하여 만든 Rx=0의 해도, 동일한 Null space에 존재하는 것을 확인할 수 있습니다. 이를 아래에서 확인해 보겠습니다.
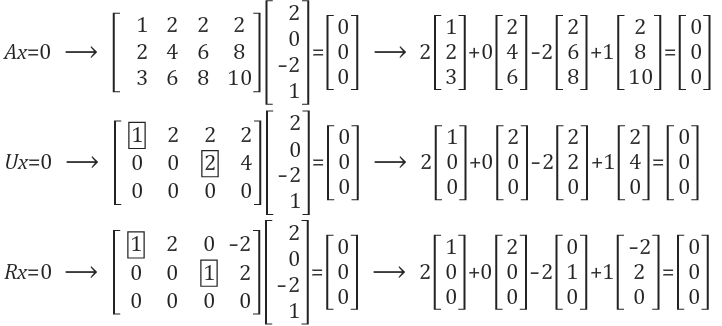
Rx=0의 해도 동일한 Null space에 존재하는 것을 알 수 있습니다. 행렬을 A에서 R로 변화시키면서, 각 행렬의 column space는 변했을지 모르나 원래 행렬에 대한 고유한 성질은 변하지 않게 됩니다. 그렇기에 해가 동일한 공간 (Null space)에 존재하게 됩니다.
■ REFERENCE
YOUTUBE LECTURE : https://www.youtube.com/watch?v=VqP2tREMvt0
인문계 공돌이: https://bizzengine.tistory.com/149
Learn Again! 러너게인: https://twlab.tistory.com/21
■ 마무리
"MIT 18.06 Linear Algebra, Spring 2005"의 7주차 "Solving Ax = 0: pivot variables, special solutions"에 대해서 정리해 봤습니다.
그럼 오늘 하루도 즐거운 나날 되길 기도하겠습니다
좋아요와 댓글 부탁드립니다 :)
감사합니다.
'STUDY > Linear Algebra' 카테고리의 다른 글
| [MIT 18.06] Lecture 9. Independence, Basis, and Dimension (0) | 2023.09.17 |
|---|---|
| [MIT 18.06] Lecture 6. Column Space and Null space (0) | 2023.09.02 |
| [MIT 18.06] Lecture 5. Transposes, Permutations, Spaces R^n (3) | 2023.08.31 |
| [MIT 18.06] Lecture 4. Factorization into A = LU (2) | 2023.08.04 |
| [MIT 18.06] Lecture 3. Multiplication and Inverse Matrices (0) | 2023.08.04 |




댓글