
안녕하세요, HELLO
오늘은 길버트 스트랭 (Gilbert Strang) 교수님의 선형대수학 강의인 "MIT 18.06 Linear Algebra, Spring 2005"에 대해서 정리하려고 합니다. 선형대수학 강의에 대한 정리와 더불어, 딥러닝을 위한 선형대수학 관점에서도 접근하여 강의를 이해하고 분석하려고 합니다.
"MIT 18.06 Linear Algebra, Spring 2005"의 4주차 "Factorization into A = LU"의 강의 내용입니다.
CHAPTER 1. 'Factorization into A = LU'
CHAPTER 2. 'How expensive is elimination'
CHAPTER 3. 'Transposes and Permutations'
CHAPTER 1. 'Factorization into A = LU'
□ 역행렬 (Inverse of Matrix)
행렬 A와 B를 곱한 결과인 AB의 역행렬은 행렬의 곱 순서가 바뀌고 각 행렬을 역행렬 해주면 됩니다.
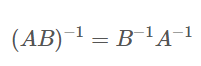
그렇다면 역행렬의 전치행렬(Transpose Matrix 행과 열을 바꿔준 행)은 아래와 같습니다.

위에서 보는 대로 첫 번째 식에서 전치를 해주면(T) 행렬 곱셈 순서가 바뀌고 각 행렬이 전치가 됩니다.
위에서 정리된 내용을 하나의 표로 정리하면 아래와 같습니다.
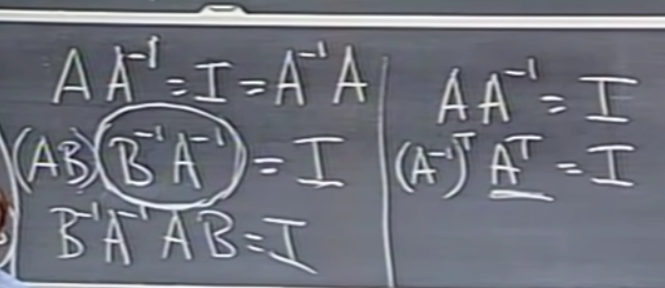
□ E = AU / A = LU (= LDU')
역행렬이 존재하는 임의의 행렬 A에 대해서, E행렬을 곱해 U행렬을 만드는 법을 배웠습니다.
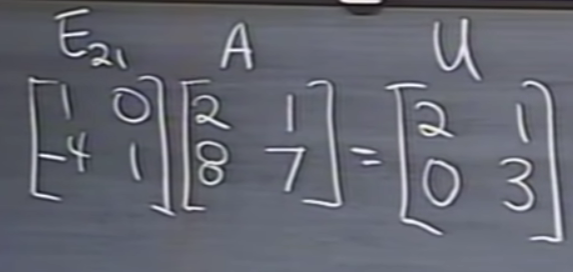
그렇다면 A=LU의 형태를 만들기 위해서는 E21의 역행렬을 좌우변에 곱해주면 된다. 그러면 A와 U를 건드리지 않고 L을 만들 수 있습니다. 이때 L은 E21의 역행렬입니다.
(둘의 관계를 유심히보면 2행 1열 원소인 -4가 4가 되었습니다, 즉 부호가 반대로 되었습니다)
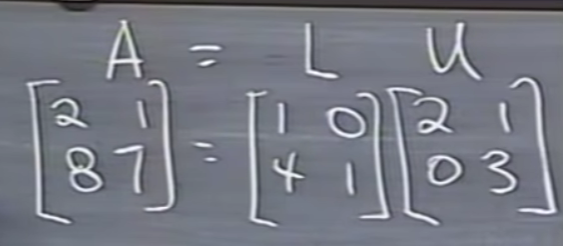
참고로 LU로 분해한 것을 다시 LDU'으로 분해할 수가 있습니다. 이때 D는 diagonal의 약자입니다.
D는 U를 pivot 값을 활용해서 행렬을 분해해 준 행렬입니다.
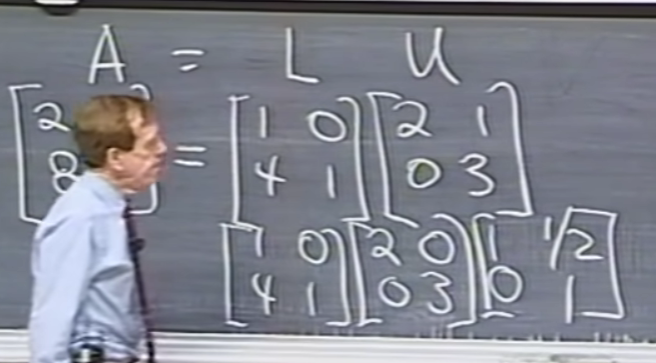
□ 2차원 이상 행렬 (e.g., 3차원 행렬)에서 계산
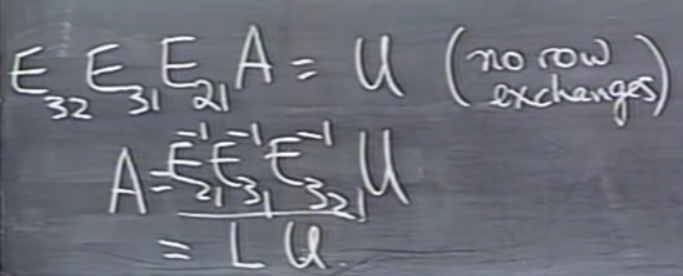
3x3 행렬은 총 3번에 걸쳐 U가 됩니다. 위와 마찬가지로 A=LU의 형태를 만들기 위해서는
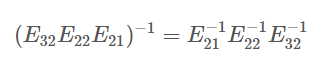
을 좌우변에 곱해줍니다. 이를 통해 A = LU 형태를 얻을 수 있습니다.
□ 그렇다면 왜 EA=U보다 A=LU가 더 좋을까요?
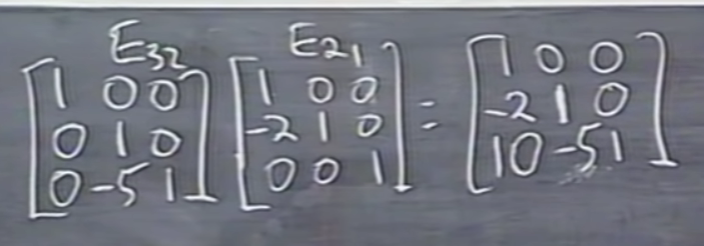
예를 들어, E32와 E21 행렬곱을 통해 E 행렬을 구해보겠습니다. (Left of A; EA = U)이 나왔다고 해보겠습니다.
이때 10이 나오는 것은 계산적으로 옳지만, 교수님은 연산에서 불편한 상황이라고 표현했습니다.
이를 아래와 같이 생각해봤습니다.
길버트 교수님은 A= LU와 A를 EA = U를 비교하였습니다. 이때 E는 치환(=순열) 행렬 (Permutation Matrix)입니다. 즉, A에 직접 행 연산을 수행하여 U로 변환하는 대신 동일한 행 연산을 E와 행렬 곱셈의 형태로 A에 적용하는 것입니다.
치환 행렬은 순서가 부여된 임의의 행렬을 의도된 다른 순서로 뒤섞는 연산 행렬로서, 일반적으로 치환행렬은 단위행렬로부터 얻을 수 있는 이진 행렬입니다.
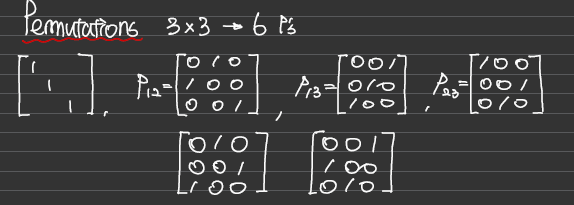
길버트 교수님의 핵심 요점은 EA = U는 올바른 결과를 생성할 수 있지만 A = LU보다 효율적이지 않다는 것입니다. 그 이유는 E를 사용함으로써 추가 계산 비용이 발생할 수 있기 때문입니다. LU 분해에서는 A에 행 연산을 직접 적용하여 U를 얻는데, 이는 E를 통해 간접적으로 동일한 연산을 적용하는 것보다 계산적으로 더 효율적일 수 있다는 점입니다. 또한 길버트 교수가 말한 요소 E(3, 1) 즉 10이 "계산은 맞지만 좋지 않다"는 말은 행 1이 추가로 제거되어 불필요한 계산 오버 헤드가 추가된다는 것으로 생각해 봤습니다.
앞에서 정리한 것처럼 행렬 A는 A = LU로 분해됩니다. 다음은 그 과정을 간략하게 설명해 보겠습니다.
- LU 분해: n x n 행렬 A가 주어지면 LU 분해는 이를 하위 삼각형 행렬 L과 상위 삼각형 행렬 U로 인수분해합니다.
- Pivoting: 실제로 partial pivoting은 수치 안정성을 보장하고 작은 수로 나누지 않기 위해 자주 사용됩니다. 여기에는 elmination 프로세스 중에 가장 큰 피벗 요소(절댓값)가 사용되도록 행을 교체하는 작업이 포함됩니다.
- Forward Elimination (순방향 제거): 이 단계의 목표는 행 연산을 사용하여 A의 주 대각선 아래의 모든 요소를 0으로 만드는 것입니다.
- Backward Substitution (역방향 치환): 행렬이 위쪽 삼각형 형태로 변환되면 역치환을 사용하여 방정식 시스템을 푸는 데 사용됩니다.
요약하면, EA = U와 A = LU 모두 올바른 결과를 얻을 수 있지만, 일반적으로 수치 알고리즘과 애플리케이션에서는 단순성과 계산 효율성으로 인해 후자가 선호됩니다. LU 분해는 원래 행렬 A에서 직접 연산하는 반면, EA = U는 추가 치환(=순열) 행렬 E를 포함하므로 추가 계산이 발생하고 프로세스가 덜 최적화될 수 있습니다.

CHAPTER 2. 'How expensive is elimination'
□ How can we solve on n x n matrix A?
데이터 엔지니어링 관점에서 U를 계산하는 것의 time complexity O(n)에 대해서 생각해 보겠습니다.
n이 100인 정방행렬을 예시로 들어보겠습니다.
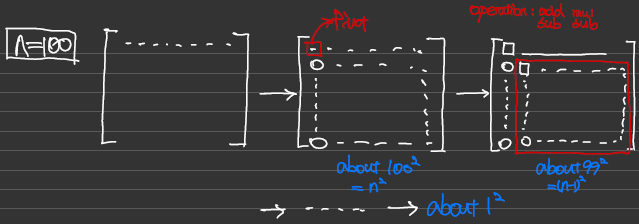
첫 번째로 첫 행에 적당한 수를 곱하고 빼는 과정이 원소의 개수만큼 있다 치면 100*100번만큼 연산이 실행됩니다.
그다음으로 첫 행과 열을 제외한 99 by 99 개의 원소에 대해, 이렇게 원소가 하나 남을 때까지 계산을 하다 보면,

n의 3 제곱에 근접하는 연산 횟수가 나온다는 사실을 알 수 있습니다.
만약 옆에 column이 하나 더 있다면, 즉 n x n이 아닌, n x m 행렬인 경우( n ≠ m)에는

시간 복잡도는 1/3*n^3 + n^2가 되는데, 이때 n이 상당히 큰 경우에는 n^2는 무시되며, n^3의 복잡도를 가지게 됩니다.
CHAPTER 3. 'Transposes and Permutations'
치환 행렬, 순열 행렬은 Permutation Matrix는 순서가 부여된 임의의 행렬을 의도된 다른 순서로 뒤섞는 연산 행렬로서, 일반적으로 치환행렬은 단위행렬로부터 얻을 수 있는 이진 행렬입니다.
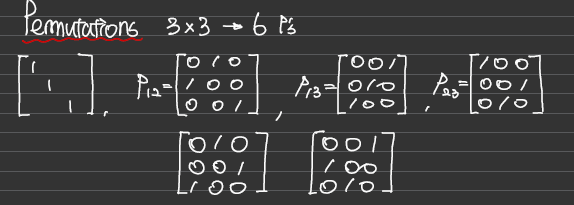
예를 들어 맨 마지막 행렬의 경우 I행렬의 1행을 2행으로, 2행을 3행으로, 3행을 1행으로 바꾼 행렬인데, 어떤 A에 곱해주면 1행이 2행, 2행이 3행, 3행이 1행으로 가게 됩니다. 서로 다른 원소들을 순서를 고려하여 일렬로 배열하는 것입니다.

P 행렬의 경우 가장 중요한 성질은 역행렬이 전치행렬과 같다는 점입니다. 즉, P에 P^T를 곱해주면 I가 됩니다. 그리고 P행렬의 개수는 n!이다.
■ REFERENCE
YOUTUBE LECTURE : URL
LECTURE BLOG : 이것 저것 공부하는 사람 Linear Algerbra(18.06) - 4. Factorization into A=LU
LECTURE BLOG : 쉽게 설명할 수 없다면 제대로 이해한 것이 아니다 - 4. Factorization into A=LU
TIME COMPLEXITY : LU 분해(LU Decomposition) - (1) 분해 과정
■ 마무리
"MIT 18.06 Linear Algebra, Spring 2005"의 4주차 "Factorization into A = LU"에 대해서 정리해 봤습니다.
그럼 오늘 하루도 즐거운 나날 되길 기도하겠습니다
좋아요와 댓글 부탁드립니다 :)
'STUDY > Linear Algebra' 카테고리의 다른 글
| [MIT 18.06] Lecture 6. Column Space and Null space (0) | 2023.09.02 |
|---|---|
| [MIT 18.06] Lecture 5. Transposes, Permutations, Spaces R^n (3) | 2023.08.31 |
| [MIT 18.06] Lecture 3. Multiplication and Inverse Matrices (0) | 2023.08.04 |
| [MIT 18.06] Lecture 2. Elimination with Matrices (5) | 2023.07.29 |
| [MIT 18.06] Lecture 1. The geometry of linear equations (0) | 2023.07.28 |




댓글