
안녕하세요, HELLO
소프트맥스 함수, softmax activiation function는 분류 작업을 위해 신경망에서 널리 사용되는 함수입니다. 이 함수는 임의의 실수 벡터를 확률 분포로 변환하며, 벡터의 각 요소는 특정 클래스의 확률을 나타내기 때문에 유용합니다.
오늘은 소프트맥스 함수에 대해서 정리하려고 합니다.
CHAPTER 1. '소프트맥스 활성화 함수 (Softmax Activation Function)' 선행 지식
CHAPTER 2. '소프트맥스 함수 (Softmax Function), 최대 함수 (Max Function)' 차이점
CHAPTER 1. '소프트맥스 활성화 함수 (Softmax Activation Function)' 선행 지식
소프트맥스 활성화 함수는 분류 작업을 위해 신경망에서 널리 사용되는 함수입니다. 이 함수는 임의의 실수 벡터를 확률 분포로 변환하며, 벡터의 각 요소는 특정 클래스의 확률을 나타내기 때문에 유용합니다.
softmax 함수는 숫자 벡터인 z를 입력으로 받아 벡터의 각 요소에 다음 공식을 적용합니다:
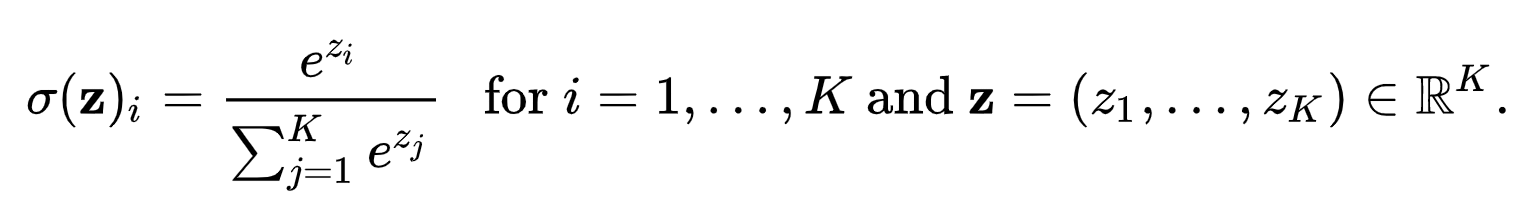
여기서 n은 벡터의 요소 수이며, softmax 함수는 입력 벡터의 각 구성 요소를 지수화한 다음 지수화된 각 값을 지수화된 모든 값의 합으로 나눕니다. 이렇게 하면 모든 확률의 합이 1이 되므로 함수의 출력이 유효한 확률 분포가 됩니다.
딥러닝에서 신경망을 훈련하는 가장 일반적인 기법 중 하나는 미적분학의 연쇄 규칙을 사용하여 네트워크의 매개변수에 대한 손실 함수의 기울기를 계산하는 역전파(backpropagation)입니다. 그런 다음 이러한 기울기를 사용하여 기울기 하강 또는 기타 최적화 방법을 통해 매개변수를 업데이트합니다.
역전파의 핵심 요건은 신경망의 모든 함수가 미분 가능해야 한다는 것입니다. 미적분학의 연쇄 법칙 (chain rule)에 따라 각 함수의 입력에 대한 출력의 미분을 계산한 다음, 이 미분을 서로 연결하여 전체 기울기를 계산할 수 있어야 하기 때문입니다.
소프트맥스 함수는 미분 가능하기 때문에 훈련을 위해 역전파에 의존하는 신경망에 사용하기에 이상적입니다. 특히, 입력에 대한 소프트맥스 함수의 미분은 다음과 같이 함수 자체로 표현할 수 있습니다:
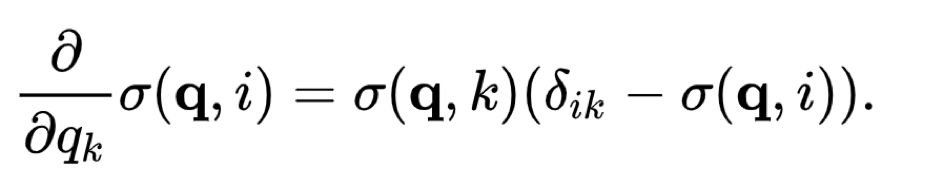
위 표현을 사용하면 소프트맥스 함수의 출력만을 사용하여 입력(즉, 신경망의 이전 계층의 출력)에 대한 소프트맥스 함수의 기울기를 효율적으로 계산할 수 있습니다. 그런 다음 이 기울기를 역전파에 사용하여 네트워크의 매개 변수에 대한 손실 함수의 기울기를 계산할 수 있습니다.
반면 max 함수는 미분할 수 없기 때문에 역전파에 의존하는 신경망에서 사용하기가 어렵습니다. 특히, 입력에 대한 max 함수의 미분은 최대 값의 지점에서 정의되지 않는데, 그 지점에는 고유한 증가 방향이 없기 때문입니다. 즉, max 함수의 기울기를 계산할 수 없으므로 역전파에 사용하기가 어렵습니다.
전반적으로 소프트맥스 함수의 차별성은 역전파에 필요한 기울기를 효율적으로 계산할 수 있기 때문에 신경망에서 소프트맥스 함수를 사용하는 데 있어 중요한 이점입니다. 반면 max 함수의 미분성이 부족하면 효율적인 최적화에 필요한 기울기를 계산할 수 없기 때문에 역전파에 의존하는 신경망에서 사용하기가 어렵습니다.
아래에서는 softmax 함수와 max 함수의 차이점에 대해서 공부한 내용을 정리했습니다.
CHAPTER 2. '소프트맥스 함수 (Softmax Function), 최대 함수 (Max Function)' 차이점
■ 딥러닝에서 소프트맥스 함수가 최대 함수보다 적절한 이유
앞에서 정리한 것처럼, max 함수는 변환 없이 단순히 벡터의 최댓값을 반환합니다. max 함수는 데이터 집합에서 가장 중요한 특징을 식별하는 것과 같은 특정 작업에는 유용할 수 있지만, 가능한 클래스에 대한 확률 분포를 제공하지 않기 때문에 분류 작업에는 적합하지 않습니다.
max 함수가 분류 작업에 적합하지 않은 주된 이유는 가능한 클래스에 대한 확률 분포를 제공하지 않기 때문입니다. 대신, 단순히 벡터의 최댓값을 반환하는데, 이는 유효한 확률일 수도 있고 아닐 수도 있습니다.
이 점을 설명하기 위해 세 개의 클래스 (A, B, C)가 있는 분류 문제를 생각해 보겠습니다.
각 클래스에 대한 점수 벡터가 다음과 같이 있다고 가정해 보겠습니다:
분류 = [A, B, C]
점수 = [2.0, 1.5, 1.0]
이 벡터에 max 함수를 적용하면 다음과 같이 됩니다:
max(scores) = 2.0
이는 최대 점수가 2.0이라는 것을 알려주지만 세 클래스의 상대적 확률에 대한 정보는 제공하지 않습니다.
반대로 같은 벡터에 softmax 함수를 적용하면 다음과 같은 결과를 얻을 수 있습니다:
softmax(scores) = [0.496, 0.333, 0.170]
이는 클래스 A의 확률이 약 0.496, 클래스 B의 확률이 약 0.333, 클래스 C의 확률이 약 0.170이라는 것을 알려줍니다. 이 확률은 모두 합쳐서 1이 되므로 세 클래스에 대해 유효한 확률 분포를 형성합니다.
소프트맥스 함수의 또 다른 중요한 장점은 미분 가능하기 때문에 신경망을 훈련하기 위한 역전파에 사용할 수 있다는 것입니다. 반면 max 함수는 미분할 수 없기 때문에 경사 기반 최적화 방법에 의존하는 신경망에서는 사용하기 어렵습니다.
◼︎ 역전파 방법을 사용하지 않는 경우, 최대 함수 사용 가능 여부
Feedforward algorithm, forward-forward algorithm 등 순방향 알고리즘과 같이 역전파에 의존하지 않는 다른 최적화 알고리즘을 사용하는 경우 활성화 함수의 차별성이 덜 중요해지며 max 함수가 소프트맥스 함수의 대안이 될 수 있습니다.
순방향 알고리즘에서는 입력 계층에서 시작하여 출력 계층으로 이동하면서 입력에 활성화 함수를 반복적으로 적용하여 네트워크의 출력을 계산합니다. 이 과정은 출력 계층에 도달할 때까지 반복되며, 이 시점에서 네트워크의 최종 출력을 얻습니다. 최적화 프로세스에는 네트워크 출력과 원하는 출력 간의 차이를 최소화하는 네트워크 매개변수 값을 찾는 과정이 포함됩니다.
이러한 맥락에서 max 함수는 분류를 수행하는 신경망의 최종 계층에 합리적인 선택이 될 수 있는데, 이는 분류 문제의 원하는 출력인 가장 높은 점수를 가진 클래스를 선택하기 때문입니다. 그러나 max 함수는 여전히 클래스에 대한 확률 분포를 제공하지 않는다는 이전과 동일한 한계를 가지고 있다는 점에 유의하는 것이 중요합니다.
또한 순방향 알고리즘에서 max 함수를 사용하는 것은 네트워크의 각 계층에 대한 활성화 함수를 반복적으로 평가해야 하기 때문에 역전파 알고리즘에서 소프트 최대 함수를 사용하는 것보다 계산 비용이 더 많이 들 수 있습니다. 반면, 역전파 알고리즘은 각 계층에 대한 활성화 함수를 한 번만 평가한 다음 기울기를 계산하고 파라미터를 업데이트하면 됩니다.
전반적으로 max 함수는 특정 최적화 알고리즘에서 소프트맥스 함수의 대안이 될 수 있지만, 확률 분포를 제공하지 못하는 한계와 잠재적으로 더 높은 계산 비용을 신중하게 고려한 후 결정해야 합니다.
◼︎ 소프트맥스 제한 사항
- 이상값에 대한 민감도 (Sensitivity to outliers): 소프트맥스는 입력 데이터의 이상값에 민감하므로 예측이 부정확할 수 있습니다.
- 미분값 소실 (Gradient saturation): 입력 값이 너무 크거나 너무 작아지면 소프트맥스 함수의 그라데이션이 포화 상태가 될 수 있습니다. 이로 인해 학습 속도가 느려지거나 학습 프로세스가 완전히 중단될 수 있습니다.
- 지배적인 클래스에 대한 편향 (Bias towards dominant classes): 소프트맥스는 입력 데이터에서 우세한 클래스에 더 많은 가중치를 부여하는 경향이 있어 소수 클래스에 대한 성능이 저하될 수 있습니다.
이러한 한계를 극복하기 위해 소프트맥스의 대안으로 몇 가지 활성화 함수가 제안되었습니다. 이러한 활성화 함수 중 일부는 다음과 같습니다:
- Rectified Linear Unit (ReLU): ReLU는 딥러닝에서 널리 사용되는 활성화 함수입니다. 이상값에 덜 민감하고 포화 없이 큰 입력 값을 처리할 수 있습니다. 하지만 0 이하 뉴런에 대해서는 학습을 중단하는 문제가 발생할 수 있습니다.
- Softplus: 소프트플러스는 "죽어가는 ReLU" 문제를 겪지 않는 부드러운 ReLU 근사치입니다. 또한 이상값에 덜 민감하며 포화 없이 큰 입력 값을 처리할 수 있습니다.
- Swish: Swish는 최근에 제안된 활성화 함수로, 여러 딥 러닝 작업에서 ReLU 및 기타 활성화 함수보다 성능이 뛰어난 것으로 나타났습니다. 이상값에 덜 민감하며 포화 없이 큰 입력 값을 처리할 수 있습니다.
- Sigmoid: 시그모이드는 일반적으로 사용되는 또 다른 활성화 함수입니다. 이상값에 덜 민감하고 포화 없이 큰 입력 값을 처리할 수 있습니다. 그러나 시그모이드는 그라데이션 소실 문제로 인해 학습 속도가 느려질 수 있습니다.
- Tanh: Tanh은 시그모이드와 유사하지만 음수 입력값을 처리할 수 있습니다. 이상값에 덜 민감하고 포화 없이 큰 입력값을 처리할 수 있습니다. 그러나 시그모이드와 마찬가지로 Tanh도 그라디언트 소실 문제가 발생할 수 있습니다.
실제로 활성화 함수의 선택은 특정 작업과 입력 데이터의 특성에 따라 달라집니다. 주어진 작업에 가장 적합한 활성화 함수를 찾기 위해 다양한 활성화 함수를 실험해 보는 것이 좋습니다.
전반적으로 max 함수는 기능 선택이나 데이터 세트에서 가장 두드러진 요소 식별과 같은 특정 작업에는 유용할 수 있지만, 가능한 클래스에 대한 확률 분포를 제공하지 않기 때문에 분류 작업에는 적합하지 않습니다. 반면, 소프트맥스 함수는 임의의 실수 벡터를 확률 분포로 변환하여 신경망이 주어진 입력에 대해 가장 가능성이 높은 클래스에 대해 정보에 입각한 결정을 내릴 수 있게 해 주기 때문에 분류 작업에 강력한 도구입니다.
■ 마무리
'소프트맥스 함수 (Softmax Activation Function)'에 대해서 정리해 봤습니다.
그럼 오늘 하루도 즐거운 나날 되길 기도하겠습니다
좋아요와 댓글 부탁드립니다 :)
감사합니다.
'DATA_SCIENCE > Deep Learning' 카테고리의 다른 글
| [딥러닝] 음성 신호 처리 (Audio Signal Processing) 기본 용어 해설, 정리, 요약 (0) | 2023.04.02 |
|---|---|
| [딥러닝] 데이터 거버넌스 (Data Governance) 해설, 정리, 요약 (0) | 2023.03.27 |
| [딥러닝] End to End model (E2E model) 해설, 정리, 요약 (0) | 2023.02.24 |
| [딥러닝] 레벤슈타인 거리 Levenshtein Distance 해설, 정리, 요약 (0) | 2023.02.21 |
| [딥러닝] 다이스 스코어 (Dice Score) 해설, 정리, 요약 (0) | 2023.02.20 |




댓글