[딥러닝] 규제 (Regularization) 해설, 정리, 요약

728x90

안녕하세요, HELLO

딥러닝은 어떤 현상에 대해서 가장 자세히 설명하기 위한 모델 함수를 찾는 것이 목적입니다. 모델을 찾을 때, 실제 정답과 모델이 예측한 결과 간의 오차가 발생하고, 정답 y와 모델이 예측값 y^과의 차이를 손실 함수 (Loss function, Cost function)이라고 합니다. 딥러닝 모델의 성능을 올리기 위해서는 손실 함수를 최소화해야 합니다.

모델에 훈련 데이터의 특징, 패턴 등이 과하게 적용되어, 손실 함수가 필요 이상으로 작아지게 되는 경우를 과적합 (Overfitting)이라고 합니다. Overfitting이 발생하게 되면 학습에 사용된 데이터에 대해서만 잘 설명하고, 다른 데이터에 대해서는 설명이 부족해지는 일반화 능력 (Generalization)이 부족해집니다. 이러한 overfitting을 해결하기 위한 방법으로는 훈련 데이터를 늘리거나, dropout, batch normalization, 모델 복잡도 낮추기 그리고 오늘 살펴볼 가중치 규제, weight regularization이 있습니다.

오늘은 모델의 overfitting을 해결해 주는 방법인 규제, regularization에 대해서 살펴보겠습니다.

CHAPTER 1. 'Bias, variance' 선행 지식

CHAPTER 2. 'Regularization' 정리

CHAPTER 1. 'Bias, variance' 선행 지식

Bias는 모델을 통해 얻은 예측값과 실제 정답과의 차이의 평균을 나타냅니다. 즉, 예측값이 실제 정답값과 얼마큼 떨어져 있는지 나타냅니다. 만약 bias가 높다고 하면 그만큼 예측값과 정답값 간의 차이가 크다고 말할 수 있습니다.

예측값과 실제 정답값과의 차이의 평균을 수식으로 나타내면 위와 같습니다.
이때, f(x)는 입력 데이터 x에 대하여 실제 정답에 해당하는 값입니다.
반면, f^(x)는 딥러닝 모델에 입력 데이터 x가 입력되었을 때, 모델이 출력한 예측값입니다. 해당 값은 모델에 따라 다양한 값을 출력할 수 있습니다.

반면 variance는 다양한 데이터 셋에 대하여 예측값이 얼마큼 변화할 수 있는지에 대한 양(Quantity)의 개념입니다. 이는 모델이 얼마큼 flexibilty를 가지는 지에 대한 의미로도 사용되며, 분산의 본래 의미와 같이 얼마큼 예측값이 퍼져서 다양하게 출력될 수 있는 정도로 해석할 수 있습니다.

variance를 수식으로 나타내면 다음과 같습니다.
분산 공식과 동일하게, 모델에서 평균과 변량의 편차를 제곱하여 나타낸 것입니다.

◆ 머신 러닝 모델과 Bias 및 Variance의 관계

bias와 variance의 크고 작음에 따라서 4가지 경우로 분류하고 머신 러닝 모델이 예측한 값들의 분포와 정답 간의 관계를 한번 살펴보도록 하겠습니다. 각 그림의 원의 중심인 빨간색이 정답 데이터의 위치라고 생각하시면 됩니다.

	Low Variance	High Variance
Low Bias	- 예측값이 정답 근방에 분포 (bias 낮음) - 예측값이 서로 몰려 있음 (variance 낮음)	- 예측값이 정답 근방에 분포 (bias 낮음) - 예측값이 서로 흩어져 있음 (variance 높음) >> Overfitting case
High Bias	- 예측값이 정답에서 떨어짐 (bias 높음) - 예측값이 서로 몰려 있음 (variance 낮음) >> Underfitting case	- 예측값이 정답에서 떨어짐 (bias 높음) - 예측값이 서로 흩어져 있음 (variance 높음)

이러한 특징을 regression, classification 예제를 통해서 확인해 보겠습니다.

■ Regression case

위 그래프에서 점선은 예측값의 regression이고, 각 점은 각 Time 값에 해당하는 정답입니다.

첫 번째 그래프는 high bias & low variance 하다고 말할 수 있습니다. high bias인 이유는 예측값이 실제 정답값과 많이 다르기 때문이고 low variance 한 이유는 예측값들의 편차가 작기 때문입니다.
두 번째 그래프는 medium bias & medium variance 하다고 말할 수 있습니다. 첫 번째 그래프에 비해 예측값과 정답값이 상대적으로 유사하지만 세 번째 그래프에 비해 오차가 크기 때문입니다. variance측면에서는 첫 번째 그래프에 비해서 예측값들의 편차가 상대적으로 커졌지만 세 번째 그래프에 비해서는 편차가 작습니다. 따라서 mideum 하다고 말할 수 있습니다.
세 번째 그래프는 low bias & high variance로 예측값과 정답이 굉장히 유사합니다. 따라서 bias는 작다고 말할 수 있습니다. 반면 모델의 예측값이 구불구불해져서 예측값들의 편차가 커졌습니다.

■ Classification case

이번에는 classification 예제를 다루어 보겠습니다.

첫 번째 그래프에서는 high bias & low variance입니다. high bias인 경우는 모델의 성능이 정답을 잘 예측하지 못하는 경우로 underfitting이 발생한 경우라고 볼 수 있습니다.
세 번째 그래프에서는 low bias & high variance가 발생하였는데, 이는 모델이 필요 이상으로 복잡하여 예측값 간의 편차가 크게 발생하는 경우입니다. 이와 같은 경우를 overfitting이 발생하였다고 볼 수 있습니다.

이와 같이 bias와 variacne는 모델의 복잡도와 관련이 있습니다. 또한 관계를 잘 살펴보면 bias와 variance는 서로 영향을 끼치고 있습니다.

bias를 낮추기 위해서 (underfitting을 개선하기 위해서) 모델의 복잡도를 높이게 되면 variance가 높아지게 되고 (overfitting이 발생) 반대로 variance를 낮추기 위해서 (overfitting을 낮추기 위해서) 모델의 복잡도를 낮추게 되면 bias가 증가 (underfitting이 발생)하게 됩니다. 적당한 수준의 bias와 variance를 만들기 위하여 적정한 수준에서 모델의 학습을 종료시켜야 합니다.

CHAPTER 2. 'Regularization' 정리

Overfitting은 모델이 훈련 데이터에 과도하게 학습되어, bias가 작고 variance가 큰 상황입니다. Regularization은 모델을 구성하는 계수(coefficients)들이 학습 데이터에 너무 완벽하게 overfitting 되지 않도록 정규화 요소(regularization term)를 더해주는 방식입니다. 손실 함수 Loss function에 규제 함수 (Regularization term)인 L1 규제 (L1 정규화, L1 Regularization, Lasso), L2 규제 (L2 정규화, L2 Regularization, Ridge)를 더하여, 손실 함수가 너무 작아져서 overfitting으로 훈련되는 것을 방지하기 위해, 가중치 weight에 페널티를 주는 기법입니다.

■ Norm 정리

두 정규화 방식의 차이점을 알기 위해 Norm이라는 개념에 대해서 정리해 보겠습니다. Norm은 유한 차원의 벡터 공간에서 벡터의 절대적인 크기(Magnitude)를 혹은 벡터 간 거리를 나타냅니다.

Norm은 특정한 속성을 만족하며, 측정 가능한 기능의 공간인 Lp 공간 (Lp Space) 혹은 르베그 공간 (Lebesgue Space)에서의 norm을 Lp norm (혹은 p-norm)이라고 합니다.

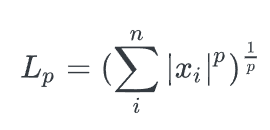
P는 norm의 차수를 의미합니다. p=1이면 L1 norm, p=2면 L2 norm입니다.
n은 대상 벡터의 요소 개수입니다.
보통 Norm은∥x∥1 또는∥x∥2와 같이 L1 norm이냐 L2 norm이냐를 구별하며, 표시가 없이 $∥ x ∥$ 처럼 차수가 표기되어있지 않으면 일반적으로 L2 norm을 의미합니다.
Norm 계산의 결과로 나오는 수치는 원점에서 벡터 좌표까지의 거리를 의미하며, 이를 magnitude라고 부릅니다.
L1, L2 정규화는 이 같은 L1, L2 norm을 사용한 값들을 더해주는 것입니다. 따라서 overfitting이 심하게 발생할 수 있는 가능성이 큰 수치에 penalty를 부여한다고 생각하면 됩니다.

■ L1, L2 Norm 차이

아래에서 L1, L2 norm에 대해서 살펴보겠습니다.

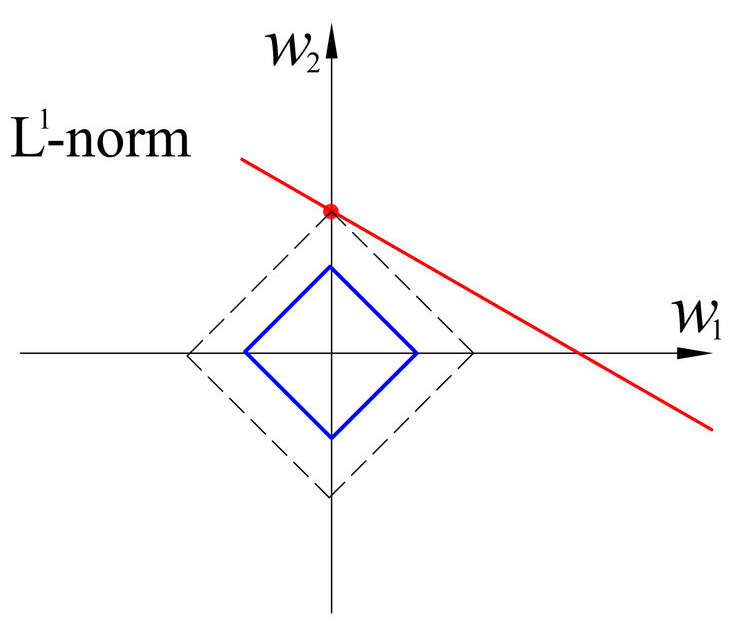
□ L1 Norm

L1 norm (Manhattan distance, Taxicab geometry), p = 1
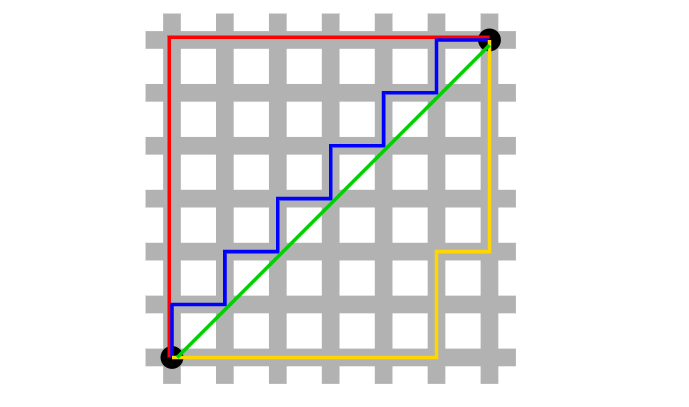
L1 norm은 맨해튼 거리 혹은 택시 거리라고 많이 알려져 있으며, 택시가 도시의 블록 사이를 이동해 다른 지점으로 이동하는 것과 같이 표현하고 있습니다.
특정 방향으로만 움직일 수 있는 조건이 있는 경우, 두 벡터 간의 최단 거리를 찾는 데 사용되는 방법입니다.
L1 loss는 아래 수식과 같이 실제 값과 예측 값 오차들의 절댓값들에 대한 합을 나타냅니다.

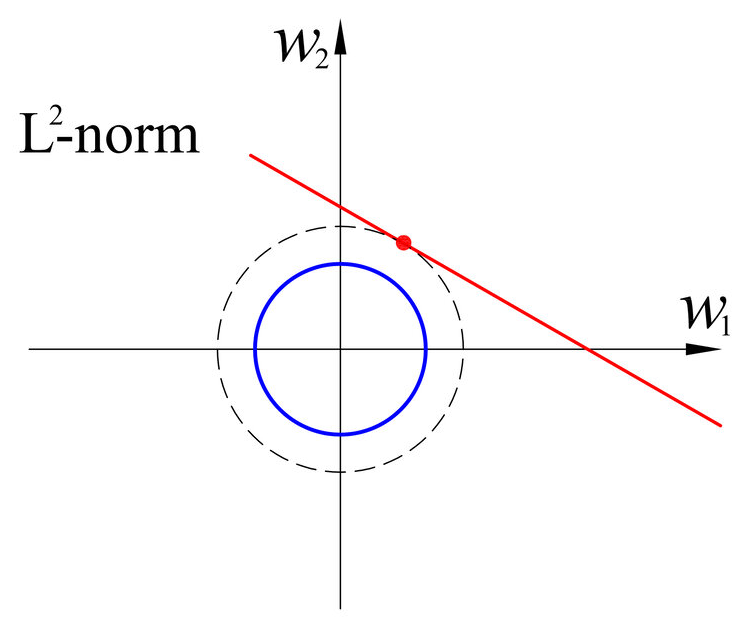
□ L2 Norm

L2 norm (Euclidean distance), p = 2
L2 norm은 유클리드 거리라고도 하며, 두 점 사이의 최단 거리를 측정할 때 사용됩니다.
L2 loss는실제 값과 예측 값 오차들의 제곱의 합으로 나타냅니다.

■ L1, L2 Regularization 차이

아래에서 L1, L2 Regularization에 대해서 살펴보겠습니다.

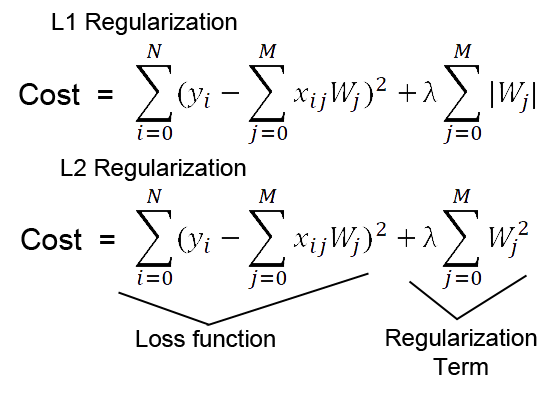
가중치에 더해주는 정규화 요소로 L1 error 절댓값을 취하는 기법을 쓰거나, L2 제곱합을 취하는 것에 따라, L1 regularization, L2 regularization으로 나뉩니다.
이때 λ (람다, lambda)는 규제에 얼마나 비중을 줄 것이 정하는 계수입니다. 0에 가까울수록 정규화의 효과는 사라집니다. 적절한 λ의 값은 k-fold cross validation과 같은 방법으로 찾을 수 있습니다.
L1과 L2 norm의 수식과 기하학적 특징에서 그 차이를 비교해 보면, L1 norm은 다른 점으로 이동하는 데에 다양한 방법이 있는 반면에, L2 norm은 단 한 가지의 방법만 있으며, L2 norm은 수식에서 오차의 제곱을 하기 때문에 outlier에 대해 더 큰 영향을 받는다는 점입니다.

추가 내용은 아래에서 확인해 보겠습니다.

□ L1 regularization

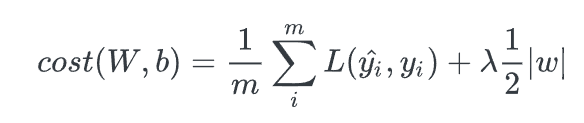
L1 Regularization (Lasso)은 기존 Cost Function에 가중치의 절댓값의 합을 더하는 형태로, 미분 시 weight의 크기에 상관없이 부호에 따라 일정한 상수값을 빼거나 더해주게 됩니다.

따라서 특정 weight들을 0으로 만들 수 있어 원하는 weight만 남길 수 있는 feature selection 역할을 할 수 있습니다. 이를 통해 특정 가중치를 삭제해 모델의 복잡도를 낮출 수 있습니다. L1 regularization을 적용한 Cost Function의 편미분 결과를 가중치 부호에 따라 가중치 값에 상수만큼 더하거나 뺄 수 있습니다.

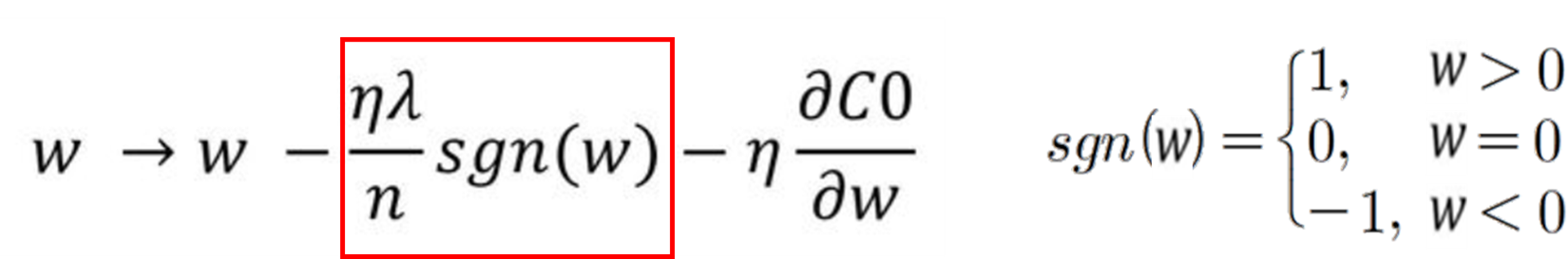
L1 norm은 다른 점으로 이동하는 다양한 방법 (feature, weight) 중 특정 방법을 0으로 처리하는 것이 가능하여 중요한 가중치만 남길 수 있는 feature selection이 가능하며, 오차의 절댓값을 사용하기 때문에 L2 대비 outlier에 좀 더 robust 합니다. 그러나 0에서 미분이 불가능해 Gradient-Based Learning 시 사용에 주의가 필요하고, 편미분 시 weight의 부호만 남기 때문에 weight의 크기에 따라 규제의 크기가 변하지 않으므로 Regularization 효과가 L2 대비 떨어집니다.

□ L2 regularization

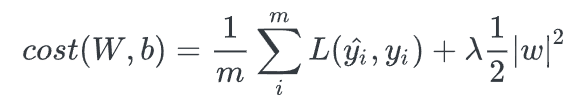
L2 Regularization (Ridge)은 기존 Cost Function에 가중치 제곱의 합을 더하는 형태로, weight의 크기에 따라 weight 값이 큰 값을 더 빠르게 감소시키는 wieght decay 기법입니다.

weight의 크기에 따라 가중치의 페널티 정도가 달라지기 때문에 가중치가 전반적으로 작아져서 학습 효과가 L1 대비 더 좋게 나타납니다. λ(람다) 값에 따라 페널티의 정도를 조절할 수 있습니다. L2 regularization을 적용한 Cost Function의 편미분 결과. 가중치의 크기에 따라 가중치 값을 감소시킬 수 있습니다.

그리고 L2 norm은 오차의 제곱을 사용하기 때문에 outlier에 대해 L1 보다 더 민감하게 작용합니다. 따라서 weight의 부호뿐만 아니라 그 크기만큼 페널티를 줄 수 있어 특정 weight가 너무 커지는 것을 방지하는 weight decay가 가능해집니다. 이러한 특징 때문에 L2 norm이 weight에 대한 규제에 좀 더 효과적이고 일반적으로 학습 시 더 좋은 결과를 얻을 수 있어 L1 norm보다 많이 사용됩니다.

■ REFERENCE

■ 마무리

오늘은 '규제 (Regularization)'에 대해서 정리해 봤습니다.

그럼 오늘 하루도 즐거운 나날 되길 기도하겠습니다

좋아요와 댓글 부탁드립니다 :)

감사합니다.

저작자표시 비영리 동일조건

'DATA_SCIENCE > Deep Learning' 카테고리의 다른 글

[딥러닝] Model-Agnostic Method 해설, 정리, 요약 (0)	2024.08.15
[딥러닝] 차원의 저주 (Curse of dimensionality) 해설, 정리, 요약 (4)	2023.10.31
[딥러닝] 음성 신호 처리 (Audio Signal Processing) 기본 용어 해설, 정리, 요약 (0)	2023.04.02
[딥러닝] 데이터 거버넌스 (Data Governance) 해설, 정리, 요약 (0)	2023.03.27
[딥러닝] 소프트맥스 함수 (Softmax Activation Function) 해설, 정리, 요약 (0)	2023.03.19