
안녕하세요, HELLO
오늘은 Leetcode 알고리즘 문제 '10. Regular Expression Matching'에 대해서 살펴보고자 합니다.
알고리즘 문제, 코드, 해설 그리고 Leetcode에서 제공해준 solution 순서대로 정리하였습니다.
STEP 1. 'Regular Expression Matching' 알고리즘 문제
STEP 2. 'Regular Expression Matching' 코드(code)
STEP 3. 'Regular Expression Matching' 해설
STEP 4. 'Regular Expression Matching' solution
STEP 1. 'Regular Expression Matching' 알고리즘 문제
Given an input string s and a pattern p, implement regular expression matching with support for '.' and '*' where:
- '.' Matches any single character.
- '*' Matches zero or more of the preceding element.
The matching should cover the entire input string (not partial).
입력 문자열과 패턴 p가 주어지면 '.'와 '*'를 지원하는 정규 표현식의 일치 여부를 판단합니다.
- '.' 모든 단일 문자와 일치합니다.
- '*' 이전 요소 중 0개 이상과 일치합니다.
일치는 전체 입력 문자열을 포함해야 합니다 (부분이 아님).
Constraints:
- 1 <= s.length <= 20
- 1 <= p.length <= 30
- s contains only lowercase English letters.
- p contains only lowercase English letters, '.', and '*'.
- It is guaranteed for each appearance of the character '*', there will be a previous valid character to match.

STEP 2. 'Regular Expression Matching' 코드(code)
■ Runtime: 68 ms, faster than 61.25% of Python3 online submissions for Regular Expression Matching.
■ Memory Usage: 14.2 MB, less than 15.44% of Python3 online submissions for Regular Expression Matching.
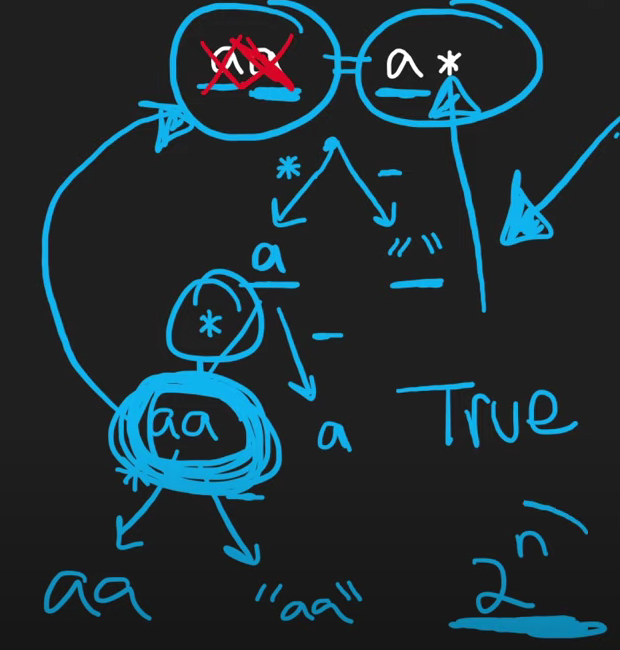
접근 방식은 패턴(p)에서 * 또는 . 여부를 검토한 후, 문자열(s)에서 맞는 지를 decision tree 모형으로 검토합니다.
기본적인 방향은 아래처럼 패턴(p)에 *이 있는 경우에는 문자열(s)에서 반복해서 단어를 검토합니다.
이때, *의 범위는 (0, ∞)입니다.
class Solution:
def isMatch(self, s: str, p: str) -> bool:
# top-down memoization
cache = {}
def dfs(i, j):
if (i, j) in cache:
return cache[(i, j)]
if i >= len(s) and j >= len(p) :
return True
if j >= len(p) :
return False
match = i < len(s) and (s[i] == p[j] or p[j] == '.')
if (j + 1) < len(p) and p[j + 1] == '*':
cache[(i, j)] = (dfs(i, j + 2) or (match and dfs(i + 1, j)))
# don't use * or use *
return cache[(i, j)]
if match:
cache[(i, j)] = dfs(i + 1, j + 1)
return cache[(i, j)]
cache[(i, j)] = False
return False
return dfs(0, 0)STEP 3. 'Regular Expression Matching' 해설
코드를 작성하면서 참고한 영상을 공유합니다.
URL: https://youtu.be/l3hda49XcDE?list=PLrmLmBdmIlpuE5GEMDXWf0PWbBD9Ga1lO
URL: https://youtu.be/HAA8mgxlov8
STEP 4. 'Regular Expression Matching' solution
추가적으로, Leetcode에서 제공해준 solution 코드를 살펴보겠습니다.
■ Runtime: 86 ms, faster than 44.29% of Python3 online submissions for Regular Expression Matching.
■ Memory Usage: 14 MB, less than 62.48% of Python3 online submissions for Regular Expression Matching.
class Solution:
def isMatch(self, s: str, p: str) -> bool:
# Initialize DP table
# Row indices represent the lengths of subpatterns
# Col indices represent the lengths of substrings
T = [
[False for _ in range(len(s)+1)]
for _ in range(len(p)+1)
]
# Mark the origin as True, since p[:0] == "" and s[:0] == ""
T[0][0] = True
# Consider all subpatterns p[:i], i > 0 against empty string s[:0]
for i in range(1, len(p)+1):
# Subpattern matches "" only if it consists of "{a-z}*" pairs
T[i][0] = i > 1 and T[i-2][0] and p[i-1] == '*'
# Consider the empty pattern p[:0] against all substrings s[:j], j > 0
# Since an empty pattern cannot match non-empty strings, cells remain False
# Match the remaining subpatterns (p[:i], i > 0) with the remaining
# substrings (s[:j], j > 0)
for i in range(1, len(p)+1):
for j in range(1, len(s)+1):
# Case 1: Last char of subpattern p[i-1] is an alphabet or '.'
if p[i-1] == s[j-1] or p[i-1] == '.':
T[i][j] |= T[i-1][j-1]
# Case 2: Last char of subpattern p[i-1] is '*'
elif p[i-1] == '*':
# Case 2a: Subpattern doesn't need '*' to match the substring
# If the subpattern without '*' matches the substring,
# the subpattern with '*' must still match
T[i][j] |= T[i-1][j]
# If the subpattern without '*' and its preceding alphabet
# matches the substring, then the subpattern with them
# must still match
T[i][j] |= i > 1 and T[i-2][j]
# Case 2b: Subpattern needs '*' to match the substring
# If the alphabet preceding '*' matches the last char of
# the substring, then '*' is used to extend the match for
# the substring without its last char
if i > 1 and p[i-2] == s[j-1] or p[i-2] == '.':
T[i][j] |= T[i][j-1]
return T[-1][-1]■ 마무리
오늘은 Leetcode 알고리즘 문제 '10. Regular Expression Matching'에 대해서 알아봤습니다.
좋아요와 댓글 부탁드리며,
오늘 하루도 즐거운 날 되시길 기도하겠습니다 :)
감사합니다.
'PROGRAMMING > LeetCode' 카테고리의 다른 글
| [Leetcode] 12. Integer to Roman_해설, 풀이, 설명 (0) | 2022.04.30 |
|---|---|
| [Leetcode] 11. Container With Most Water_해설, 풀이, 설명 (1) | 2022.04.27 |
| [Leetcode] 9. Palindrome Number_해설, 풀이, 설명 (0) | 2022.04.18 |
| [Leetcode] 8. String to Integer (atoi)_해설, 풀이, 설명 (0) | 2022.04.06 |
| [Leetcode] 7. Reverse Integer_해설, 풀이, 설명 (0) | 2022.04.06 |




댓글