
안녕하세요, HELLO
오늘은 DeepLearning.AI에서 진행하는 앤드류 응(Andrew Ng) 교수님의 딥러닝 전문화의 두 번째 과정인 "Improving Deep Neural Networks: Hyperparameter Tuning, Regularization and Optimization"을 정리하려고 합니다.
"Improving Deep Neural Networks: Hyperparameter Tuning, Regularization and Optimization"의 강의 목적은 '랜덤 초기화, L2 및 드롭아웃 정규화, 하이퍼 파라미터 튜닝, 배치 정규화 및 기울기 검사와 같은 표준 신경망 기술' 등을 배우며, 강의는 아래와 같이 구성되어 있습니다.
~ Practical Aspects of Deep Learning
~ Optimization Algorithms
~ Hyperparameter Tuning, Batch Normalization and Programming Frameworks
"Improving Deep Neural Networks" (Andrew Ng)의 1주차 "Setting up optimization problem"의 강의 내용입니다.
CHAPTER 1. 'Normalizing Inputs'
CHAPTER 2. 'Vanishing and exploding gradients'
CHAPTER 3. 'Weight initialization for deep networks'
CHAPTER 4. 'Numerical approximation of gradients'
CHAPTER 1. 'Normalizing Inputs'
□ Normalize inputs
■ 정규화 방법

- 테스트 세트를 정규화할 때 훈련 데이터에 사용한 평균(μ)과 표준편차(σ)를 사용합니다.
- 정규화를 통해 비용 함수의 모양은 둥글고 최적화하기 쉬운 모습으로 됩니다. 이를 통해 학습 알고리즘이 빨리 실행됩니다.
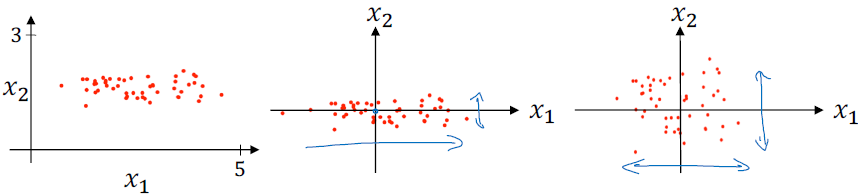
□ Why normalize inputs
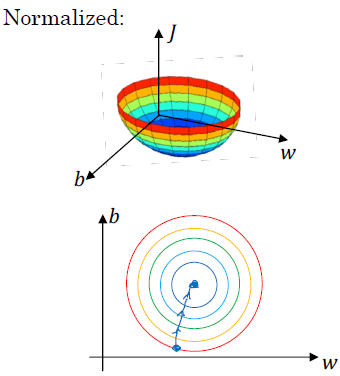
정규화되지 않은 값에 대해서 비용 함수는 아래 그림처럼 길쭉한 비용 함수 모양입니다. (elongated cost function) 정규화하지 않는 데이터에 대해서는 경사 하강법(gradient descent)을 적용할 경우, 많은 시행 횟수를 통해 최적화 과정이 이뤄집니다.

반면에 정규화를 하게 되면, 가중치(w)와 편차(b)의 관계는 정규화하지 않은 데이터에 비해 대칭적인 형태(symmetric feature)를 가집니다. 그리고 경사 하강법(gradient descent)을 적용할 경우, 적은 시행 횟수를 통해 최적화 과정이 이뤄집니다.
CHAPTER 2. 'Vanishing and exploding gradients'
□ Vanishing and exploding gradients
깊은 신경망을 훈련시킬 때 나타나는 문제점은 '경사의 소실과 폭발'입니다. 깊은 신경망에서 가중치 w가 단위행렬(1)을 보다 크면 (예를 들어 1.5), 신경망 개수(L)에 따라 계속해서 곱해지며, 예측값은 매우 큰 값을 가지게 됩니다. 반면에, 작으면 (예를 들어 0.5) 신경망 개수(L)에 따라 계속해서 곱해지며, 예측값은 매우 작은 값을 가지게 됩니다.
이를 토대로 생각하면 경사 하강법에서 w의 값이 단위행렬보다 큰 값이면 경사의 폭발, w의 값이 단위행렬보다 작은 값이면 경사의 소실 문제점이 생깁니다.

CHAPTER 3. 'Weight initialization for deep networks'
경사 소실 및 폭발을 막기 위해서 '가중치 초기화(weight initialization)'를 하고 가중치를 1보다 너무 큰 수나 너무 작은 수를 하지 않도록 해주어 폭발이나 소실을 막아줍니다. 즉, 결괏값 z가 폭발적인 값 또는 작은 값을 가지지 않기 위해서는 깊은 신경망(large n)인 경우에는 작은 가중치(smaller w)가 필요합니다

CHAPTER 4. 'Numerical approximation of gradients'
□ Check derivative computation
경사 검사를 하는 이유는 역전파를 알맞게 구현했는지 확인하기 위함입니다.
이를 위한 방법에는 중심 차분법이 있습니다. 앱실론(ε)은 극한에서 매우 작은 숫자를 의미합니다.
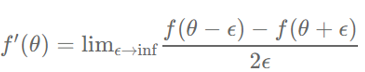
이때 예측 오차(approximation error)는 앱실론 제곱의 오차만큼 나타난다.
□ Gradient checking (Grad check)

1. 벡터로 변환해서, 자이언트 벡터 theta로 바꿔줍니다.
2. gradient도 마찬가지로, 자이언트 벡터 derivation theta로 바꿔줍니다.
2-1. x1과 dx1은 동일한 차원(dimenstion)입니다.
3. J는 자이언트 파라미터의 비용 함수입니다.
유클리안 거리를 활용해서 deriavtive approximate와 derivateive theta 두 벡터의 차원에서 거리를 구합니다.
일반적으로 10의 -7승을 앱실론 값으로 둘 때, 두 벡터 간의 거리가 10의 -7승보다 작으면 approximate 값이 derivate와 유사하다고 할 수 있으며, 반면에 앱실론 값보다 큰 경우에는 벡터의 구성 요소를 다시 한번 검토해야 될 필요가 있습니다.
□ Gradient checking implementation notes
경사 검사(Gradient check) 방법은 속도가 굉장히 느리기 때문에 훈련 시에는 사용하지 않고 디버깅할 때만 사용합니다.
알고리즘이 경사 검사에 실패했다면, 어느 원소 부분에서 실패했는지 찾아봅니다. 특정 부분에서 계속 실패했다면, 그 경사가 계산된 충에서 문제가 생긴 것을 확인할 수 있습니다.
드롭아웃에서는 무작위로 노드를 삭제하기 때문에 적용하기 쉽지 않습니다. 따라서 드롭아웃을 끄고 알고리즘이 최소
한 드롭아웃이 없는지 확인하고, 다시 드롭아웃을 진행합니다.
■ 마무리
'Improving Deep Neural Networks'의 1주차 "Setting up optimization problem"에 대해서 정리해봤습니다.
그럼 오늘 하루도 즐거운 나날 되길 기도하겠습니다
좋아요와 댓글 부탁드립니다 :)
감사합니다.
'COURSERA' 카테고리의 다른 글
| week 1_Initialization 실습 (Andrew Ng) (0) | 2022.02.18 |
|---|---|
| week 1_Practical Aspects of Deep Learning 연습문제 (Andrew Ng) (0) | 2022.02.18 |
| week 1_Regularization neural network (Andrew Ng) (0) | 2022.02.16 |
| week 1_Setting up machine learning application (Andrew Ng) (1) | 2022.02.16 |
| [COURSERA] Improving Deep Neural Networks: Hyperparameter Tuning, Regularization and Optimization (Andrew Ng) (0) | 2022.02.14 |




댓글